FastFA: A Unicode Enabled Regex Engine for Code Generators
Updated on 2021-12-25
Explore, run, and manipulate DFA regular expressions from graphs, to state machines with this library
Introduction
Let me start off with something of a disclaimer. This article is of niche interest. FastFA is already used in Reggie and Rolex. Using those tools requires no direct knowledge of FastFA, and can produce source code for running regular expressions, making this article of more interest to those who are curious about how it all works, or maybe someone who wants to make their own source code generator with it. It can also help in understanding the two projects I mentioned better.
That said, this iteration of FastFA is newer than the versions shipped with the aforementioned projects, and while compatible, this version adds features.
What the Heck Is It?
In short, FastFA is a regular expression engine. Unlike most regular expression engines, this one is not geared towards runtime use. It can be used at runtime, but it's more efficient to use it to generate source code that can then run the regular expression for you. Projects like Reggie use it to compute the code that needs to be generated. FastFA does not generate code by itself. Rather, it produces data that can be used to orchestrate code generation by other applications.
What's With the Name?
You might be wondering what FA is, or why it isn't called "Regular Expression Engine" or similar. The thing is, as conceived these don't have to match characters. You can potentially use it to match other streams. The ability to match regular expressions presents one - albeit the far most common - use case. FA means Finite Automata in this case which are special classes of state machines meant for matching patterns, usually - but not always - in text.
Why Not Just use System.Text.RegularExpressions?
- That engine is more expressive, but not as efficient since it backtracks, while this one does not. It's not uncommon to see a more than double improvement in execution time.
- That engine is opaque, meaning you have little control over the internals and no control over the actual code generation. This engine is transparent, exposing the necessary information at all levels necessary to run matches or generate source code that runs matches.
- That engine does not directly support lexing/tokenization, which is a special way to use regular expressions to do compound pattern matching. This one does.
- Sometimes, it's simply nice to have something you can tinker with and take apart.
Acknowledgements
Portions of this code in the file FFA.cs were derived from code created by other authors, and similarly licensed under MIT
- Fare, Copyright (C) 2013 Nikos Baxevanis itself ported from
- dk.brics.automaton, Copyright (c) 2001-2011 Anders Moeller
You can find the full copyright notices in FFA.cs
Understanding this Mess
Wow. We have some ground to cover. I'll try to break this up as best as I can.
What Is a Regular Expression, Exactly?
A regular expression is a tiny functional language (kind of like LISP or F#, but much simpler) with a relatively small number of basic operators that match patterns in text. You cannot use a non-backtracking regular expression to match any sort text that nests or otherwise creates a heirarchy. Here is a tutorial for working with regular expressions. The category of "languages" that regular expressions can recognize are known as "regular languages" or Chomsky type 3 languages.
This particular engine is POSIX(ish). It doesn't support every feature, but it supports all the ones you're most likely to use except for anchors. I haven't implemented anchors yet because they are problematic.
How Does It Work?
If you prefer mathematical formalisms, you may want to give this a read.
A non-backtracking regular expression can be transformed into a derivative state machine that can match text.
The state machines in their final form are very simple. The transition function of such a state machine accepts a single character (technically a UTF-32 codepoint) and - assuming one can be found, returns a new state and advances the input by one character. Each state may be accepting or non-accepting. In some cases, states may also have an "accept symbol id" that is a numeric value associated with an accepting state, but most of the time we don't need that. In the case where the transition function does not find a next state, if the current state is accepting, it is a match.
Consider the following directed graph:
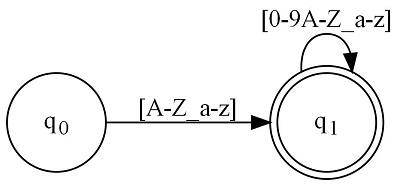
This is a simple state machine matching a C identifier. It was generated using the following regular expression: [A-Z_a-z][0-9A-Z_a-z]*
Each circle in the graph represents a state. The name or handle of the state which we can use to refer to it is printed in the middle. Graphs always begin with q0. In this case, we have two circles on the graph representing the set of states { q0, q1 }. You'll note that q1 is double circled. That means it is an accepting state. When in that state, if there are no more moves available either because end of input was reached, or there are otherwise no suitable/matching inputs, this is a match.
The black arrows that lead away from a state collectively represent that state's transition function. Basically, they indicate where you move. Above each black arrow is a regular expression fragment that is either a character or ranges of characters indicating which inputs can move along the associated arrow. Remember whenever we move along an arrow, we also advance the input cursor by one.
When you have no more moves available or you're out of input, check the current state for a double circle. If it's double circled, this is an accepting state, and therefore a match. Otherwise, it's not a match.
The above is for matching text. Tokenizers are these same state machines with a slight twist. Every double circled /accepting state has an associated integer symbol id that indicates exactly what was matched. That associated id is reported whenever a match occurs.
But How Do You Get That Graph From an Expression?
First, the closure of a state is said to be all the states reachable from this state along any arrow directly or indirectly, including itself. The closure of a state represents a complete state machine. Therefore, the closure of each state within that closure also represents a state machine, and so on. It's almost like Russian nesting dolls, but this is a directed graph, not a tree. In the C identifier figure from above, there is the state machine beginning at q0, and technically, also one at q1, which handles the latter part of the overall match.
The above is important because it highlights the composability of these state machines. You can build little machines to run part of your match, and then create a larger machine that references those machines. If we do it this way, we can break down any regular expression into a few basic building blocks which we stick together like Legos to make the complete machine.
In fact, this method of composing state machines out of a small set of foundational machines is known as Thompson's construction. This is done during the parsing process, or by using Thompson construction methods exposed by the API.
Using this Mess
The Main API
The central type is F.FFA in FastFA.dll. This represents a single state in a state machine. However, it also exposes the entire API through its interface. Remember that I mentioned the closure, which is the set of all states reachable from this state directly or indirectly by following the arrows. You can compute the closure from any given state to get a set of all the states in its entire machine. Therefore, you can think of an instance of an FFA as either a single state, or the root state of a state machine depending on what you need in the moment. They work the same way either way. Many of the operations you perform on a state treat that state as the root state of a state machine. For example, calling IsMatch() on one will match an input string using that instance as the root of the state machine.
Typically, you will parse a regular expression into an FFA instance using FFA.Parse() at which point you can analyze its Transitions, or more typically, analyze its transition ranges by destination state using FillInputTransitionRangesGroupedByState() which is useful for code generators. You can also get the machine as a packed int[] array using ToDfaTable(). If you want the state machine back as a regular expression, you can call ToString(). If you want to get a graph of it, make sure you have GraphViz installed and in your path and then use RenderToFile() or RenderToStream().
Aside from parsing, you can build state graphs from UTF32 codepoints directly using the static Thompson construction methods like Literal(), Set(), Repeat(), Concat() and Or().
Here's an example of using it:
// our expression
var exp = "foo|(bar)+|baz";
Console.WriteLine(exp);
// parse it
var fa = FFA.Parse(exp);
// write it back as an equivalent regular expression
Console.WriteLine(fa);
// run IsMatch
Console.WriteLine("IsMatch(\"foo\") = {0}", fa.IsMatch("foo"));
// run IsMatch (DFA table)
Console.WriteLine("IsMatch(dfa, \"barbar\") = {0}", FFA.IsMatch(fa.ToDfaTable(), "barbar"));
// run searches
var srch = "abcde foo fghij barbar klmnop baz";
var lc = LexContext.Create(srch);
Console.WriteLine("Search(\"{0}\")", srch);
var pos = 0L;
// run Search
while (-1 < (pos = fa.Search(lc))) {
Console.WriteLine("\t{0} @ {1}", lc.GetCapture(), pos);
}
lc = LexContext.Create(srch);
Console.WriteLine("Search(dfa, \"{0}\")", srch);
pos = 0L;
// run Search (DFA table)
while (-1 < (pos = FFA.Search(fa.ToDfaTable(), lc))) {
Console.WriteLine("\t{0} @ {1}", lc.GetCapture(), pos);
}
// C identifier:
var ident = FFA.Parse("[A-Z_a-z][A-Z_a-z0-9]*");
var opts = new FFA.DotGraphOptions();
// don't need to see accept symbol ids
opts.HideAcceptSymbolIds = true;
// render it to a jpg in the project directory
// this is used in the article!
ident.RenderToFile(@"..\..\..\ident.jpg",opts);The DFA Table Layout
When packed as an integer array, the DFA table is built so that it can be efficiently navigated. It is stored as follows:
You have a list of states, where each state consists of an accept id (-1 for not accepting), followed by a count of transitions, followed by each transition.
Each transition in turn, starts with a destination state index. This is the absolute index into dfa table array where the next state begins. It is not the state number, like qN. Following that is a count of packed ranges, and the packed ranges themselves follow.
Each packed range consists of a minimum input value and a maximum input value - typically the UTF32 codepoints that make up the range, at least when using the state machine for matching regular expressions (though remember you can technically use it for matching things other than text.)
Anyway, just to show you what I mean, here's code for taking a LexContext over an input, and checking if its contents can be matched by our DFA state table:
public static bool IsMatch(int[] dfa, LexContext lc) {
lc.EnsureStarted();
int si = 0;
while (true) {
// retrieve the accept id
var acc = dfa[si++];
if (lc.Current == LexContext.EndOfInput) {
return acc != -1;
}
// get the transitions count
var trns = dfa[si++];
var matched = false;
for (var i = 0; i < trns; ++i) {
// get the destination state
var tto = dfa[si++];
// get the packed range count
var prlen = dfa[si++];
for (var j = 0; j < prlen; ++j) {
// get the min cp
var min = dfa[si++];
// get the max cp
var max = dfa[si++];
if (min > lc.Current) {
// we need to break.
// first advance si
// past the remaining
// packed ranges
si += (prlen - (j+1)) * 2;
break;
}
if (max >= lc.Current) {
// the new state
si = tto;
matched = true;
// break out of both loops
goto next_state;
}
}
}
next_state:
if (!matched) {
// is the state accepting?
if (acc != -1) {
return lc.Current ==
LexContext.EndOfInput;
}
return false;
}
lc.Advance();
if (lc.Current == LexContext.EndOfInput) {
// is the current state accepting?
return dfa[si] != -1;
}
}
}It looks a little hairy at first with all the dfa[si++] nonsense but what it's doing isn't complicated at all. It's just reading the next value out of the array, si being the current array index into dfa. I've commented above everywhere it's pulling relevant data out of the DFA table. That's the key to reading the state table, whether you're doing it to match, or doing it to generate code. In many instances, you can simply use the array instead of using the entire FastFA library, eliminating a need for a dependency, and increasing overall efficiency.
Search() and IsMatch()
These methods allow you to do two of the three major things you can do with regular expressions. Specifically, they allow you to find matching text within a larger stream, and they allow you to check whether the text matches the expression respresented by the state machine.
IsMatch() should be obvious. Search() is almost as simple, except it can be called multiple times over the same stream until a negative number is returned. You have to feed it an LC.LexContext, from LexContext.dll. You can create one by calling LexContext.Create() and feeding that method some text.
Of these, the static DFA table methods will be the most efficient, while the others are provided mostly for ease, and also because frankly, it made it easier for me to debug, and I saw little reason to remove them.
Where's the Tokenizing/Lexing?
The one thing it won't allow you to do is to tokenize text. I decided against providing that, not so much for effort and maintenance reasons but because for starters, I already provide two tokenizer generators that use FastFA, and Reggie was released pretty recently, so I recommend using it. It will generate C# source code for you that can search, validate, or tokenize based on the regular expressions you give it. Also, to tokenize requires the introduction of more types or at least tuples and additional buy in to support features like Rolex's and Reggie's "block end" feature that are almost necessary in the real world. By the time you're done, you're talking about a significant amount of API surface area that is introduced, and also dependency-wise, it adds a burden. Reggie sidesteps most of those issues by generating the source code for you, so the runtime engine doesn't need to muck about in the tokenization arena, and your generated code doesn't need a runtime. Everything is happy. Do keep in mind that while I recommend using Reggie for this, this iteration of FastFA is slightly newer and has additional features (including Search()! and Match()!). Reggie uses this engine (albeit the last version of it) to work its magic, so you may as well just use that. Code generated by Reggie is not dependent on FastFA.dll or LexContext.dll.
Points of Interest
One of the new features I've included is the ability to call ToString() on an FFA instance and get a regular expression back. This works using the DFA state removal method, or at least my best effort attempt at it after years of never getting it right. It has managed to work with everything I've thrown at it so far, but it has not been used in the wild yet, so caveat emptor. Sometimes, what it generates won't be pretty, but it should match the same thing it was given, regardless. It's pretty interesting how that works. You can poke around in the FFA.cs labyrinth for ToString() if you want to see it. There is a lot to it though, so beware.
History
- 25th December, 2021 - Initial submission