FSM Explorer: Learn Regex Engines and Finite Automata
Updated on 2024-01-02
This article presents a program to help visualize regular expression mechanics.
Introduction
See my follow up article at this link for a newer version of this library that supports compilation, as well as an explainer on how that all works.
A while ago, I wrote an article on how regular expression engines work. Here is a second attempt at that. Some of the content is carried over from the other article. In addition to an explainer here, a solution is provided with a regular expression engine and an explorer application that automates Graphviz to show you how it works.
how regular expression engines work
Prerequisites
- A PC with Windows and a recent version of Visual Studio
- Graphviz installed and in your PATH
Update: Added option to view optimized DFA with the application
Update 2: Improvements to the FA engine, and bugfixes
Conceptualizing This Mess
This article assumes passing familiarity with common regular expression notation. You don't have to be an expert, but knowing what ?, *, +, |, [], and () do is very helpful. If you only know a subset, that's okay too, as long as you understand the basic idea behind regular expressions and what they're for.
What you might not know, is the theory behind their operation, which we'll cover here.
At its core, a regular expression is a finite state machine based on a directed graph. That is to say, it is a network of nodes, connected to other nodes along directional paths. This is easier to visualize than to describe:
finite state machine directed graph
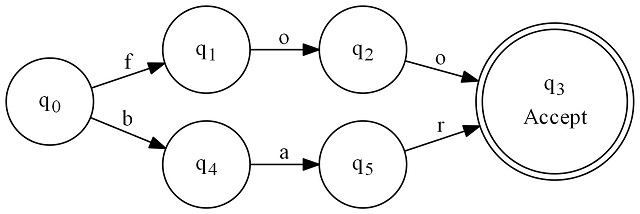
This regular expression graph matches "foo" or "bar". The regular expression for this would be foo|bar.
Here's how it works: We always start at q0. From there, we have a series of black arrows pointing away. Each one is labeled with a character. Well, we examine the first character of the string to match. If it is "f" we proceed to q1. If it is "b" we proceed to q4. Any time we move along a black arrow, we increment the input string's cursor position by one. On q1 or q4, we will be examining the next input character, and so on. This continues until we can no longer match any characters. If at that point, we are on a state with a double circle (an "accepting state"), we have matched. If we are on some single circle state at that point, then we have not matched.
We can create these graphs based on parsing a regular expression, and then use code to "run" these graphs, such that they can match input strings.
Speaking of matching, there are two significantly different ways to use a regular expression engine. The first, and perhaps the most common is to scan through a long string of text looking for certain patterns. This is what you do in the Search and Replace dialog in Visual Studio if you enable regular expression matching for example. This is well covered ground for Microsoft's regular expression engine, and it is generally best practice to use it in these cases. For long strings, it can outperform our library since it implements things like Boyer-Moore searches whereas ours does not. Generally, it's a good idea to rely on Microsoft's engine for this style of matching.
The other way to use a regular expression engine is called tokenizing. This basically moves through an input stream, and it attempts to match a string under the cursor to a particular pattern, and then it reports the pattern that was matched, before advancing. Basically, it uses a compound regular expression (combined with ors) and matches text to one of the particular expressions - and tells you which one it was that matched. This is very useful for lexers/tokenizers which are used by parsers. Microsoft's regular expression engine is not suited to this task, and attempts to use it for this come with a number of disadvantages including additional code complexity and a considerable performance hit. This gap in functionality is enough to justify a custom regular expression engine if one is crafting parsers or tokenizing for some other reason.
Unlike Microsoft's regular expression engine, this engine does not backtrack. That is, it will never examine a character more than once. This leads to better performance, but non-backtracking expressions aren't quite as expressive/powerful as backtracking ones. Things like atomic zero width assertions are not possible using this engine, but the trade-off is more than worth it, especially when used for tokenizing.
Returning to the graphs, as alluded to, each one of these represents a finite state machine. The state machine has a root always represented by q0. If we were to take any subset of the graph, like, say starting at q4 and ignoring anything not pointed to directly or indirectly by q4, then that is also a state machine. Basically, a finite state machine is a set of interconnected state machines!
To find your entire state machine from the node you're presently on, you take the closure of a state. The closure is the set of all states reachable directly or indirectly from some state, including itself. The closure for q0 is always the entire graph. In this case, the closure for q4 is { q4, q5, q3 }. Note we never move backward along an arrow. The graph is directed. Taking the closure is a core operation of most any finite state machine code.
Let's move on to a slightly more complicated example: (foo|bar)+. Basically, we're just adding a loop to the machine so it can match "foobarfoo" or "foofoobar" or "barbarfoofoobar", etc.
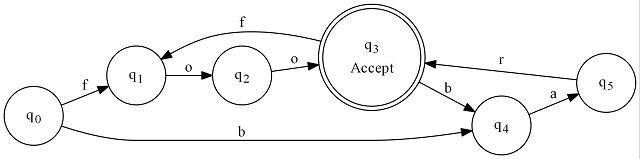
This graph looks totally different! If you follow it however, it will make sense. Also note that we have outgoing arrows from the double circled accepting state. The implication is such that we do not stop once we reach the accepting state until we can't continue - either because we can't find the next character match or because we ran out of input. We only care that it's accepting after we've matched as much as we can. This is called greedy matching. You can simulate lazy matching with more complicated expressions but there is no built in facility for that in non-backtracking regular expressions.
Building these graphs is a bit of a trick. The above graphs are known as DFAs but it's much easier to programmatically build graphs using NFAs. To implement NFAs, we add an additional type of line to the graph - dashed lines, we call epsilon transitions. Unlike input transitions, epsilon transitions do not consume any input or advance the input cursor. As soon as you are in a state, you are also in every state connected to it by a dashed line. Yes, we can be in more than one state at once now.
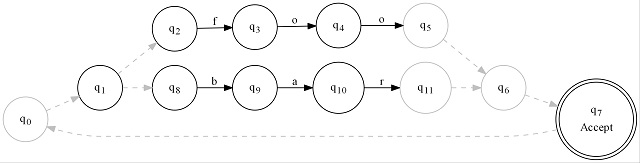
Two things that immediately stand out are the addition of the gray dashed lines and how much more intuitive the graph is. Remember that I said you automatically move into the states connected by epsilon transitions which means as soon as you are in q0, you are also in q1, q2, and q8. It can be said that the epsilon closure of q0 is { q0, q1, q2, q8 }. This is because of the dashed arrows leading out from each of the relevant states.
The above graph is much more expensive for a computer to navigate than the one that precedes it. The reason is that those epsilon transitions introduce the ability to be in multiple states at once. It is said to be non-deterministic.
The former graph is deterministic. It can only be in one state at a time, and that makes it much simpler for a computer to navigate it quickly.
An interesting property of these non-deterministic graphs is there's essentially one equivalent deterministic graph. That is, there is one equivalent graph with no dashed lines/epsilon transitions in it. In other words, for any NFA there is one DFA that is equivalent. We'll be exploiting this property later.
Now that we know we can create these NFAs (with epsilon transitions) and later transform them to DFAs (without epsilon transitions), we'll be using NFA graphs for all of our state machine construction, only turning them into DFAs once we're finished.
We're going to use a variant of Thompson's construction algorithm to build our graphs. This works by defining a few elemental subgraphs and then composing those into larger graphs:
First, we have a literal - regex of ABC:
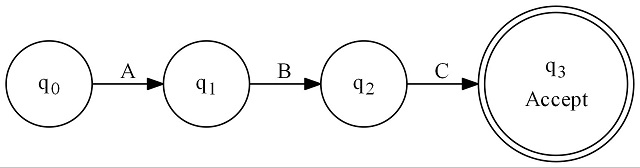
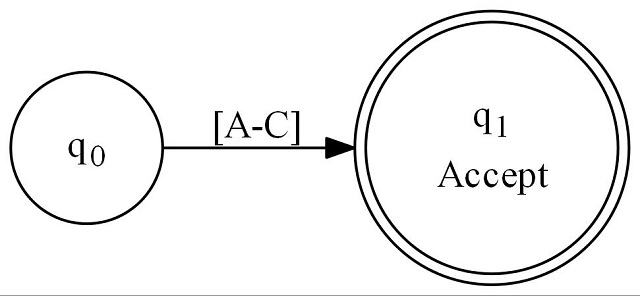
Next, we have a character set - regex of [ABC]:
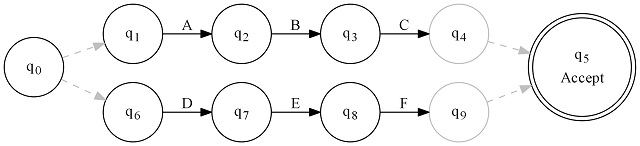
Next, we have concatenation - regex of ABC(DEF): (this is typically implicit)

Now, we have or - regex of ABC|DEF:
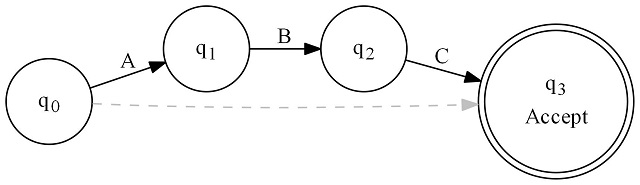
Next we have optional - regex of (ABC)?:
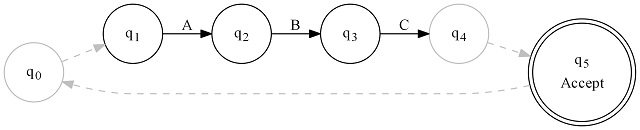
Finally, we have repeat - regex of (ABC)+:
Every other pattern you can do can be composed of these. We put these together a bit like legos to build graphs. The only issue is when we stick them together, we must make the former accepting states non accepting and then create a new accepting state for the final machine. Repeat this process, nested to compose graphs.
Note the grayed states with only a single outgoing dashed line. These are neutral states. They effectively do not do anything to change what the machine accepts, but they are introduced during the Thompson construction. This is fine, as it is a byproduct that will be eliminated once we transform the graph to a DFA.
Final states meanwhile, are simply states that have no outgoing transition. Generally, these states are also accepting.
These finite state machines are the heart of our regular expression engine.
Subset construction once again, is how we turn an NFA into a DFA. We like this, because DFAs are much more efficient as we'll see later. What we need to do basically, is figure out all of the possible combinations of states we can be in. Each set of possible states will resolve roughly to one DFA state. The exception is when it's impossible such that two states transition to destination different states on the same input. At that point, we end up exploding the possibilities because we need to clone the path N-1 times where N is the number of conflicts. This is not easy to explain nor particularly easy to code. Hopefully, a couple of figures will help.
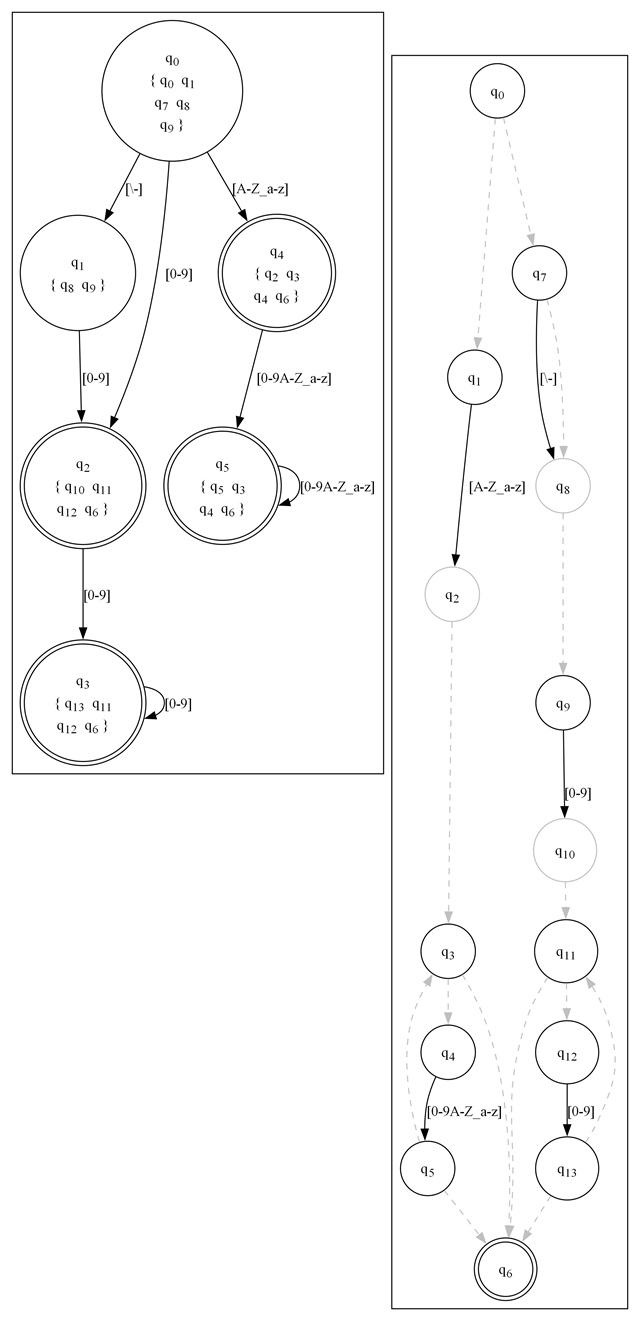
The graph indicates the NFA on the right, and on the left it shows which of the source states the DFA state is composed of. You'll see that each state encompasses several of the other states. Sometimes however, a couple of states can yield a lot more states under the right - or rather wrong circumstances. Note that subset construction can sometimes yield duplicate states which can be removed through an optimization process.
Using the Application
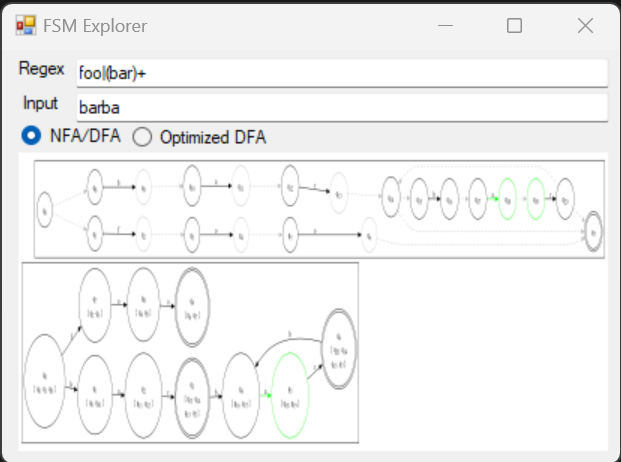
After installing GraphViz (ensuring it puts it in your PATH), you can launch the FSM Explorer application.
Enter the regular expression in the top textbox. The regular expression will then be transformed into both an NFA and a DFA, respectively, and shown in the application. The current state(s) are highlighted using green. As you enter input, the current state(s) will change.
Note that the DFA is not optimized. Elimination of duplicate states prevents showing the subset construction due to the algorithm used. The subset construction is the list of states from the top graph that make up the state in the bottom graph. Each set is listed in its associated DFA state.
You can optionally choose to view the optimized DFA instead of the NFA and DFA together.
History
- 21st December, 2023 - Initial submission
- 22nd December, 2023 - Added option to view optimized DFA
- 2nd January, 2024 - API improvements and bug fixes