Fun With State Machines: Incrementally Parsing Numbers Using Hacked Regex
Updated on 2021-01-02
Hoodwink your computer into doing your work for you using regular expressions
Introduction
And now for something completely different. This article was inspired by a recent coding adventure of mine wherein I set out to solve a problem. How can I parse a number of indefinite length, that may be too large to hold in memory at once? atoi() and strtod() fall down here. You might suspect I was writing an arbitrary precision library. I was not, but this could be adapted to one, because the principles in here are similar in terms of parsing. My goal was to present a best effort numeric approximation of a JSON number in value space, while also preserving it in lexical space for the purpose of round tripping. For example, if you had pi to one million digits, there's no way you're holding that in value space at least with standard floating point. At best, you can approximate it. However, there's no reason you shouldn't be able to preserve that entire number as a string of characters, especially if you can stream it in chunks. But how do you do both at the same time? I needed to solve that problem, and now I'll show you how I did it.
Prerequisites
- You'll need a computer that isn't presently on fire.
- Hopefully it has a C++ compiler on it.
- It should also have .NET on it. I use MonoDevelop on Linux, but the code in question - or maybe I should say the questionable code - will run on Windows and work from Visual Studio.
- Speaking of the code, you'll need the code from this article since that's what I'm using to generate the C# state machine we'll be porting. It's dusty code, but it's perfect for this. I've provided a link to it above as well.
- You'll want to install Graphviz probably, at least if you want a pretty flow chart to go along with the state machine. It's better than staring at a
switchwrapped around a bunch ofifstatements.
Conceptualizing this Mess
I love state machines. If I can solve a problem with one, I get giddy. The trouble with them is they're murder to maintain so I prefer to make the computer deal with that where possible, though that's not always possible. Even then however, I can use the computer to help me write the code, which I can then modify. The generated code is ugly, but at least there aren't bugs until I touch it.
In this case, we're going to use a state machine to make a sort of coroutine - a restartable method. They have these in C++20 but spoiler alert, the compiler builds state machines in your code to make them work. Since I was targeting C++11 for reasons, I don't have those. C++20 is relatively new, so you may not either. If you do, well aren't you fancy! You can skip this mess, unless you're interested, but with your shiny new compiler you have less hackish options.
A coroutine basically is a method that is broken up iteratively. It performs one piece of its total function each time its called. A traditional function is called once, performs an entire unit of work and then returns. A coroutine is called multiple times, each time performing a small fraction of its work before returning control to the caller. Coroutines are useful for cooperative multithreading because they don't typically block for long periods. They are also useful for something very similar - iteratively parsing, and that's what we'll be doing. They are sort of "asynchronish" in that they are effectively non-blocking, but more importantly for us, they can handle their work a small bit of data at a time, which means we can for example, read a character from the disk, parse it, and then move to the next value, and repeat.
As I said, I prefer to cajole my computer into doing my work for me whenever possible, because it's a better programmer than I am, in terms of the number of bugs it tends to avoid. Plus I'm lazy.
I'm not above threatening my computer, but I find it's more effective to resort to trickery to get it to do what I want. In this case, I'm going to fool it into thinking it's generating pretty graphs and C# code for matching regular expressions. What it's really doing is giving me a blueprint for the state machine I don't want to write from scratch, and giving me a flowchart to keep track of it to boot.
At around the time I realized that a state machine* and a regular expression were pretty much interchangable and convertible from one form to the other mathematically, I decided I really liked regular expressions. They're basically a really abbreviated functional programming language with just a few basic operators: ()|?* and the rest is syntactic sugar or backtracking which is different animal. The article I linked to earlier gives you a rundown of the operators but I cover them at the end of the article here as well. The output of such an expression is a state machine. We'll be exploiting that.
- I took a liberty. Specifically, this applies to two classes of finite state machine - DFAs and NFAs, not all state machines. I claim literary license.
In case you missed it, we'll be using a regular expression to create the basis for a coroutine.
And in case there weren't enough clowns in this particular circus, we're going to create that coroutine in C# and then get the computer to port it to C using yet more regular expressions. It's regular expressions all the way down.
Finally, we're going to augment it with logic to accumulate parsed characters into a number.
It all starts with the regular expression: (-?)(0|[1-9][0-9]*)((.[0-9]+)?([Ee][+-]?[0-9]+)?)
This represents a valid JSON number. It must not have extra leading zeroes. It must not have a leading . It may have a fractional part and an exponent part. The exponent part can be specified like E10, E+10, or e-10.
If you look at the regular expression, you can see some of those rules in there, if you squint. I got good at them because I have odd hobbies.
Anyway, it might be easier with a pretty little diagram:
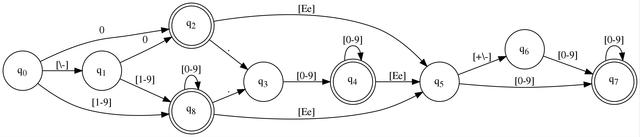
This is Chutes and Ladders®! Follow the black lines whenever you see one of the characters that appears above it, where \ is just an escape and [0-9] indicates a range of digits. Every time you advance to a new bubble, you advance your input by one, so for example, you'd call fgetc() one time to get the next character. You keep going until you have no more moves. If when you are done, you landed on a double circle, you win. Otherwise, you lose. I'm kidding. The double circle means the value we just read was valid. If we have to stop and we're not on a double circle, that means it was invalid.
Now, I'm going to tell you that the graph was generated from that regular expression. The question is, are you the type of person who would just trust a total stranger like that? If you don't believe me - and perhaps you shouldn't, as I've been known to exaggerate - then read the article I posted in the prerequisites section, as it gives a pretty thorough treatment of the process.
Meditate on the graph. There's code there, if you squint. Think about it. It's a goto table. Each bubble represents a label you can goto, and each line represents a condition upon which you advance. The implicit part is the comparand of the condition, which is the current character off the input source you're reading. Every time you follow a line (goto), you advance the input by one.
Keep that in mind so what I'm about to show you doesn't come off as witchcraft. I've been accused of that before, and it's always incredibly awkward.
Using this Mess
Let's start by unboxing that old codebase. Go to the RegexDemo project and mercilessly lay waste to the code in the Project.cs's Main() function quickly and with conviction - before it has a chance to live.
var fa = RegexExpression.Parse(@"(\-?)(0|([1-9][0-9]*))
((\.[0-9]+)?([Ee][\+\-]?[0-9]+)?)").ToFA<string>();
fa.RenderToFile(string.Join(Path.DirectorySeparatorChar.ToString(),
new string[] { "..", "..", "flt_nfa.jpg" }));
fa = fa.Reduce();
fa = fa.ToDfa();
fa.TrimDuplicates();
// HACK: Apparently there's an old bug in my DFA table creation.
// It doesn't matter because I have a new algo anyway but this code
// is ancient. We just correct the output here:
// remove all transitions from q2 to q4
var cl = fa.FillClosure();
var q2 = cl[2];
var q4 = cl[4];
var l = q2.FillClosure();
var r = new List<char>();
foreach(var f in l)
{
// get our transitions dictionary backward
var d = (IDictionary<CharFA<string>, ICollection<char>>)f.InputTransitions;
ICollection<char> c;
if (d.TryGetValue(q4, out c))
{
foreach (var ch in c)
{
r.Add(ch);
}
}
}
foreach(var ch in r)
{
q2.InputTransitions.Remove(ch);
}
fa.RenderToFile(string.Join(Path.DirectorySeparatorChar.ToString(),
new string[] { "..", "..", "flt_dfa.jpg" }));
var dfaTable = fa.ToDfaStateTable();
var method = CharFA<string>.GenerateLexMethod(dfaTable, -1);
var cd = CodeDomProvider.CreateProvider("c#");
var w = new StringWriter();
cd.GenerateCodeFromMember(method, w, new CodeGeneratorOptions());
var s = w.ToString().Replace("context.CaptureCurrent();" + Environment.NewLine, "");
s = s.Replace(" context.Advance()", "*pch = fgetc(pfile)");
s = s.Replace("context.Current", "*pch");
s=Regex.Replace(s, "goto q([0-9]+);",
"*pstate = $1;" + Environment.NewLine + " return 1;");
s = s.Replace("goto q", "*pstate = ");
s = s.Replace("return 0;", "*paccept = 1;\r\n return -1 != *pch;");
s = s.Replace("error:" + Environment.NewLine, "}"+Environment.NewLine+"error:" +
Environment.NewLine + " ");
s = s.Replace("context.EnsureStarted();", "switch(*pstate) {");
s = s.Replace(" // q0", "case 0:");
s = Regex.Replace(s,"q([0-9]+):", "case $1:");
s = s.Replace("return -1;", "return 0;");
s = s.Replace("internal static int Lex(RE.ParseContext context)",
"#include <stdio.h>\r\n#define LEXNUM1\r\nint lexnum
(FILE* pfile,int* pstate,int* pch,int* paccept)");
s = Regex.Replace(s,@"if \(\(\*pch == '([0-9]|\.|\-|E|e|\+)'\)\)", @"if (*pch == '$1')");
Console.WriteLine(s);Replace it with this. Add the usings it yells about like System.Text.RegularExpressions at the top of the file. The weird array things in RenderToFile() are to build paths for Windows users, because they are ... different. It will dump flt_nfa.jpg and flt_dfa.jpg to your RegexDemo project directory, but only if you have GraphViz installed. Otherwise, it will complain if you don't comment the RenderToFile() lines out and learn to live without the pictures. Of the two, the latter one is more directly useful, but is also proportionately more confusing. It was generated from the former one, which represents the same flow, but in an easier to follow way. The gray dashed lines are moved to on no input. Once again, see the article I linked to for information on reading the NFA graphs. Or don't. Go ahead and make me sad.
The replaces are used to convert the C# code to C. We only need a couple of regular expressions in here, but I challenge anyone who says they aren't immensely useful to fisticuffs. That's what this whole mess is about. We just used them to teach the computer C and it isn't even that bright.
Note: Astute readers, and by those I mean the ones not currently nursing a serious head injury have probably noticed a rather nasty hack in the above code. "HACK:" being our subtle clue. The ToDfa() routine is apparently dodgy and generates incorrect DFAs ... sometimes. Otherwise, I would have caught it before this article... maybe. Anyway, in this case, it creates erroneous transitions from q2 to q4 which should not exist. I remove them in the code. You may commence with the public shaming, as I've earned it. I have long since moved on to a new algorithm that is much faster and more importantly, correct - because I didn't come up with it. Plus it handles Unicode which we didn't need here, but it generates tables, not code, which isn't very useful for us in this situation. I will eventually produce a code generator for C and C++ which avoids all of this in the first place.
Anyway, it dumps some grotty looking code to the console. You'll want to paste it into your favorite the least terrible C++ editor you have because we're going to tinker with it:
#include <stdio.h>
#define LEXNUM1
int lexnum(FILE* pfile,int* pstate,int* pch,int* paccept) {
switch(*pstate) {
case 0:
if (*pch == '-') {
*pch = fgetc(pfile);
*pstate = 1;
return 1;
}
if (*pch == '0') {
*pch = fgetc(pfile);
*pstate = 2;
return 1;
}
if (((*pch >= '1')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 8;
return 1;
}
goto error;
case 1:
if (*pch == '0') {
*pch = fgetc(pfile);
*pstate = 2;
return 1;
}
if (((*pch >= '1')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 8;
return 1;
}
goto error;
case 2:
if (*pch == '.') {
*pch = fgetc(pfile);
*pstate = 3;
return 1;
}
if (((*pch == 'E')
|| (*pch == 'e'))) {
*pch = fgetc(pfile);
*pstate = 5;
return 1;
}
*paccept = 1;
return -1 != *pch;
case 3:
if (((*pch >= '0')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 4;
return 1;
}
goto error;
case 4:
if (((*pch == 'E')
|| (*pch == 'e'))) {
*pch = fgetc(pfile);
*pstate = 5;
return 1;
}
if (((*pch >= '0')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 4;
return 1;
}
*paccept = 1;
return -1 != *pch;
case 5:
if (((*pch == '+')
|| (*pch == '-'))) {
*pch = fgetc(pfile);
*pstate = 6;
return 1;
}
if (((*pch >= '0')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 7;
return 1;
}
goto error;
case 6:
if (((*pch >= '0')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 7;
return 1;
}
goto error;
case 7:
if (((*pch >= '0')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 7;
return 1;
}
*paccept = 1;
return -1 != *pch;
case 8:
if (*pch == '.') {
*pch = fgetc(pfile);
*pstate = 3;
return 1;
}
if (((*pch == 'E')
|| (*pch == 'e'))) {
*pch = fgetc(pfile);
*pstate = 5;
return 1;
}
if (((*pch >= '0')
&& (*pch <= '9'))) {
*pch = fgetc(pfile);
*pstate = 8;
return 1;
}
*paccept = 1;
return -1 != *pch;
}
error:
*pch = fgetc(pfile);
return 0;
}The formatting is slightly awful but you can fix it by tabbing out the body of the switch with your editor, or using its fancy auto format feature if you have one. Save it as lexnum1.h in your project.
Remember how I said each bubble is represented with a label? Don't worry, I wouldn't lie to you (without sufficient incentive.) They have now been replaced by case x where x is the id of the state, so q0 is case 0. Our range expressions [...] have been replaced with >= and <= comparisons in if tests. Otherwise, single character comparisons are done with == and taken together, they represent the lines in the graph. We're using fgetc() to fetch characters off the input for the purpose of the demonstration. Obviously, using fgetc() is pretty limiting, but the reason I chose it is it is easy to replace with something else. Its return values and overall usage couldn't be more simple, and easy to emulate. I'm trying to do you a solid over here. When we land on a double circle state, we set *paccept to a non-zero value, and only suggest to read more characters if we didn't get an EOF signal from fgetc(). This code is kind of confusing so later we'll be using the jpg the computer made to help us follow it.
One wrinkle is that fgetc() advances and returns the next character, while the C# code called Advance() which reads the next character into Current. That means we both have to call fgetc() once first to "prime" the machine with a starting character (which is what EnsureStarted() did under the covers anyway in the C# code), and also we must keep the last character we read around as part of the machine state to replace what used to be Current.
Also, the original C# code wasn't a coroutine - in an actual coroutine instead of goto, we would need to return, and pick up where we left off next time. This is accomplished by keeping a pstate parameter around, and replacing the labels with a switch(pstate), and a case for each label. It's a direct translation, because this was already a state machine, it was just built so it executes entirely within one call to the routine, and we used simple string matching to change that above. That's how direct the translation is.
However, we need to add our actual parsing code in there to make it worthwhile. By that, I mean we need to have code that turns streams of characters coming from fgetc() into numbers, because who doesn't love numbers? The state machine's associated jpg graph actually makes that easy. We can identify lines in the graph where we need to do certain things like multiply by 10 and then add the next digit, and so that tells us where in that nasty code we must put our calculations.
Work work work. I know, but imagine you wrote that nonsense by hand. Not only would you have to defend yourself against a particularly brutal and possibly violent code review, parsing numbers seems easy until you have to do it. There are a lot of corner cases to keep track of. If you don't let the computer generate this code, that means you have to do it, and who needs that kind of abuse? Luckily, our computers are gullible and can be convinced to do most of our work for us.
First, I'll save you the hassle of actually following along and downloading the code that accompanies the article by putting the driver code in main.cpp right here, because the essence of coding is copy and paste, or so I've learned from the Q&A section:
#include <stdio.h>
#include "lexnum1.h"
#ifdef LEXNUM1
int main(int argc,char** argv) {
// create one char strings:
char sz[2];
sz[1]=0;
int state = 0;
int accept = 0;
FILE* pfile = fopen("pi.txt","r");
if(!pfile) {
printf("Could not open pi.txt\r\n");
return -1;
}
int ch = fgetc(pfile);
if(0>ch) {
printf("pi.txt was empty\r\n");
fclose(pfile);
return -1;
}
sz[0]=ch;
printf("%s",sz);
// lexnum is a coroutine. we call it repeatedly
// and each time it performs just on character
// of the parse. It's done when it returns 0
while(lexnum(pfile,&state,&ch,&accept)) {
if(-1<ch) {
sz[0]=ch;
printf("%s",sz);
}
}
printf("\r\n");
if(0!=accept) {
printf("Accepted number\r\n");
} else {
printf("Rejected number\r\n");
}
fclose(pfile);
}
#endifThere's the magic we're after. Now we can verify the number in a streaming fashion, character by character.
We need to create pi.txt and put 3.141592653589793238462643 in it, although anyone that memorizes that much pi is probably anti-social, which is why I picked it up as a teen.
Now when we run it, we get:
Accepted numberAnd if we mangle the number in pi.txt, we get:
Rejected numberYay, progress!
Of course, verification isn't really the endgame. We want to parse this thing into value space - a numeric representation. In order to do so, we need an accumulator and some additional state. Rather than add yet more parameters to the lexnum() function, let's change it so it takes a struct. While we're at it, we'll add that extra information to it, and then I'll get to explaining it after the fact, because I'm just difficult like that:
struct lex_info {
FILE *pfile;
int state;
int ch;
int accept;
int neg;
int overflow;
double value;
int frac_count;
int e_neg;
int e_count;
};This is what we now pass to lexnum() in lexnum2.h. You'll find the corresponding pfile, state, ch and accept, but we have several new pieces of data. I created lexnum2.h from lexnum1.h through the magic of Search and Replace, a modern miracle. That would have been even easier to just do initially with the C# code prior, but I broke it up into seperate steps for the demo. That's all I'm going to cover of that because that's all that was done for this iteration of lexnum(). You'll find the new driver code in main.cpp, and the corresponding header in the project.
These hold enough information to keep track of where we are in the parse, and what our accumulated value is so far. To be honest, using ints for everything is overkill - we could get away with a 6 bit frac_count and then 1 bit for neg and one for overflow, for example, but I didn't want to complicate the demo. neg tells us if the number is negative, frac_count tells us how many fractional digits we've parsed so far, overflow tells us it was too big to accurately represent in value space, e_neg tells us whether the e_count is negative, and e_count holds our the number after the e, if any.
Now we're going to modify the state machine, because who doesn't love revisiting the same piece of code only to rewrite bits of it? Still, this is better than doing the whole thing from scratch. You know you agree with me.
This time, we're going to add the code that uses all of those values. What we can do is refer to the graph to figure out where we are and what we need to parse. Then we add the parsing code to the appropriate transition under the associated state. I just wrote that to confuse you, but now let me show you, because I'm a nice person.
We can start with q0. This is probably a good place to zero out our struct, so we'll add code to do that there, under case 0. After that, according to the state diagram, we have one of three possibilities. A zero, one through nine, or a hyphen. You can see in the code we have the relevant ifs that represent the transitions. It's under these that we put the code:
case 0:
pinfo->accept = 0;
pinfo->e_count = 0;
pinfo->e_neg = 0;
pinfo->frac_count = 0;
pinfo->neg = 0;
pinfo->overflow = 0;
pinfo->value = 0.0;
if (pinfo->ch == '-') {
// set our negative flag
pinfo->neg = 1;
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 1;
return 1;
}
if (pinfo->ch == '0') {
// do nothing, value is already 0
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 2;
return 1;
}
if (((pinfo->ch >= '1')
&& (pinfo->ch <= '9'))) {
// "parse" our number into value
pinfo->value = pinfo->ch-'0';
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 8;
return 1;
}
goto error;That one gets us started, but I'll show you another, where we do some of the accumulation. How about the fraction parts in q3? Why not?
case 3:
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
// parse the fraction digits (after .)
// we only parse up to 63 because
// a double isn't likely to be
// more precise than that anyway
if(pinfo->frac_count<63) {
cp=pinfo->ch-'0';
if(0!=pinfo->neg)
cp=-cp;
// turn 1-9 into .1-.9 or .01-.09 or whatever
// depending on frac_count. Then add it to
// the result
pinfo->value+=(cp*(pow(10, (pinfo->frac_count * -1))));
// increment the frac_count
++pinfo->frac_count;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 4;
return 1;
}
goto error;That's just a little bit of math. I'm not even good at math, but I came up with that through trial and error. I'm a bit slow sometimes, but I make up for it with tenacity.
Now, we go through each state, and under each transition, we parse the relevant bit, adjusting the value accumulator based on the values of the other members. In the real world, this would be done iteratively, testing each part as you build it, but I really wanted a montage and this is as close as I can get:
For the full effect, play this while looking at the code:
Montage Soundtrack
int lexnum(lex_info* pinfo) {
int cp;
if(0!=pinfo->accept && 0>pinfo->ch)
goto accepted;
switch(pinfo->state) {
case 0:
pinfo->accept = 0;
pinfo->e_count = 0;
pinfo->e_neg = 0;
pinfo->frac_count = 0;
pinfo->neg = 0;
pinfo->overflow = 0;
pinfo->value = 0.0;
if (pinfo->ch == '-') {
// set our negative flag
pinfo->neg = 1;
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 1;
return 1;
}
if (pinfo->ch == '0') {
// do nothing, value is already 0
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 2;
return 1;
}
if (((pinfo->ch >= '1')
&& (pinfo->ch <= '9'))) {
// "parse" our number into value
pinfo->value = pinfo->ch-'0';
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 8;
return 1;
}
goto error;
case 1:
if (pinfo->ch == '0') {
// do nothing. value is already 0
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 2;
return 1;
}
if (((pinfo->ch >= '1')
&& (pinfo->ch <= '9'))) {
// "parse" a digit into value
// will always be negative from
// here
pinfo->value = -(pinfo->ch-'0');
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 8;
return 1;
}
goto error;
case 2:
if (pinfo->ch == '.') {
// now increment our frac count
++pinfo->frac_count;
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 3;
return 1;
}
if (((pinfo->ch == 'E')
|| (pinfo->ch == 'e'))) {
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 5;
return 1;
}
pinfo->accept = 1;
return 1; // -1 != pinfo->ch;
case 3:
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
// parse the fraction digits (after .)
// we only parse up to 63 because
// a double isn't likely to be
// more precise than that anyway
if(pinfo->frac_count<63) {
cp=pinfo->ch-'0';
if(0!=pinfo->neg)
cp=-cp;
// turn 1-9 into .1-.9 or .01-.09 or whatever
// depending on frac_count. Then add it to
// the result
pinfo->value+=(cp*(pow(10, (pinfo->frac_count * -1))));
// increment the frac_count
++pinfo->frac_count;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 4;
return 1;
}
goto error;
case 4:
if (((pinfo->ch == 'E')
|| (pinfo->ch == 'e'))) {
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 5;
return 1;
}
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
// we're doing the exact same thing
// here we did in state 3/q3
if(pinfo->frac_count<63) {
cp=pinfo->ch-'0';
if(0!=pinfo->neg)
cp=-cp;
pinfo->value+=(cp*(pow(10, (pinfo->frac_count * -1))));
++pinfo->frac_count;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 4;
return 1;
}
pinfo->accept = 1;
return 1; // -1 != pinfo->ch;
case 5:
if (((pinfo->ch == '+')
|| (pinfo->ch == '-'))) {
if('-'==pinfo->ch) {
// use this to determine E is
// negative instead of positive
pinfo->e_neg = 1;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 6;
return 1;
}
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
cp=pinfo->ch-'0';
// we accept up to SOMETHINGe+1000000
if(pinfo->e_count>1000000) {
// we overflowed
pinfo->overflow = 1;
} else {
// add the next digit to e
pinfo->e_count=pinfo->e_count*10+cp;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 7;
return 1;
}
goto error;
case 6:
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
// same as state 5
cp=pinfo->ch-'0';
if(pinfo->e_count>1000000) {
// we overflowed
pinfo->overflow = 1;
} else {
// add the next digit to e
pinfo->e_count=pinfo->e_count*10+cp;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 7;
return 1;
}
goto error;
case 7:
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
// same as state 5
cp=pinfo->ch-'0';
if(pinfo->e_count>1000000) {
// we overflowed
pinfo->overflow = 1;
} else {
// add the next digit to e
pinfo->e_count=pinfo->e_count*10+cp;
}
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 7;
return 1;
}
pinfo->accept = 1;
return 1; // -1 != pinfo->ch;
case 8:
if (pinfo->ch == '.') {
// increment our frac count
++pinfo->frac_count;
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 3;
return 1;
}
if (((pinfo->ch == 'E')
|| (pinfo->ch == 'e'))) {
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 5;
return 1;
}
if (((pinfo->ch >= '0')
&& (pinfo->ch <= '9'))) {
// "parse" a digit:
cp = pinfo->ch-'0';
if(pinfo->neg)
cp=-cp;
// we have to fudge a little to avoid
// rounding errors
pinfo->value = floor(pinfo->value*10.0+0.5)+cp;
pinfo->ch = fgetc(pinfo->pfile);
pinfo->state = 8;
return 1;
}
pinfo->accept = 1;
return 1; // -1 != pinfo->ch;
}
error:
pinfo->ch = fgetc(pinfo->pfile);
return 0;
accepted:
// do the final math to fixup the number
if(0<pinfo->e_count) {
double p = pow(10,pinfo->e_count);
if(0!=pinfo->e_neg) {
// it's negative
pinfo->value/=p;
} else {
pinfo->value*=p;
}
}
return 0;
}I've deliberately left the switch unindented so that despite the formatting, you can actually read it on this site without wrapping absolutely every line. I've also added a bit of a hack to the coroutine wherein before it runs the state machine, it checks to see if we're on end of input, and if we've accepted already. If so, it jumps to accepted: where it finalizes the numeric computations. To help facilitate this, I've also made it so the accepting states always return 1 instead of returning 1 only if we're not on EOF. The upshot of this is the last time you call lexnum(), the final number will be computed. This hack will only work in situations where the lexer can use EOF as the ending condition. Most real world lexing routines must support at least some other sorts of ending conditions. Usually what happens is it will simply stop once it can't move along a black arrow in the graph anymore. That's the ending condition. It's kind of permissive because it means 3.14x5 will stop with a valid result just before "x", but we like permissive here because it's just another way of saying flexible (morally or otherwise) am I right? Still, for the demo I didn't do that, because then we'd have to handle that in the driver code, and it adds complexity without being illustrative. The code is complicated enough.
Now when running the code, we get this:
3.141592653589793238462643
Accepted number: 3.141593It also appropriately rejects invalid numbers.
With that, we've completed what we set out to do, by which I mean engaging in questionable practices to fulfill a task of niche value.
How to Regex
First, don't use it as a verb. I did because I have trouble with authority. Anyway, regex is just abbreviated operations that define a pattern of text. We'll cover non-backtracking regex since it's more useful to us than the alternative, and it's simpler. It all starts with some core operators.
Core Operators
(abc)- a subexpression. This works the same way it does in any language, in that it overrides precedence. Capturing matches also use parantheses to dictate a portion of text to capture while matching, but don't worry about that, because capturing is an extra feature, and not part of core regular expressions.abc- concatenation. Matches "abc", ora,b, and finallycin series. You'll notice this doesn't have an operator. It's simply implicit.a|b|c- alternation. Matchesaorborc. Precedence for|is such thatabc|def|ghiworks as expected, in that it matches either "abc", "def" or "ghi".(abc)?- match the expression to the left zero or one times. Here, it matches "abc" zero or once. Note we needed parentheses because normally?will only match the character to the left due to operator precedence.(abc)*- kleene star. Matches "abc" zero or more times. Valid strings include "", "abc", "abcabc" and "abcabcabcabcabc"
Like operators in any language, they are compositional - you use them as building blocks of larger expressions which also use them, and so on. There are also common operators which are shorthand for the operators above.
Common Syntactic Sugar
[a-c]- matches a set of characters. The prior matches once character, which can be eithera, orborc. It could have also been written as[abc]. The longhand is(a|b|c).[^a-c]- matches any single character excepta,borc. The longhand is too long to write out here, but it would be like(d|e|f|g|...)and all the control charagers, digits and symbols - everything buta,b, orc.(abc)+- matches the expression one or more times. This would match "abc" or "abcabc" but not "". The longhand for this would be(abc)(abc)*.
Conclusion
I wouldn't want to leave you without anything so hopefully I've conveyed several ideas.
- Regular expressions are a simple, not scary, functional programming language whose output is a DFA state machine
- As such they can be used to match text, or to generate code to run DFA state machines
- The code that generates the regex state machines can create documentation by way of state graphs, and this can compensate for the ugliness of the generated code
- Getting the computer to generate complicated code may not save you work up front, but it pays huge dividends on the back end by cutting down on bugs and making testing easier. For example, we can be fairly certain that the state machine will reject strings that do not match our initial regular expression without testing all of those cases.
- It's okay to abuse old code in order to make it useful again.
- Your computer is basically dumb, but eager. If you set your scruples aside in the name of expediency, you can con it into doing things it would never otherwise agree to.
History
- 2nd January, 2020 - Initial submission