GLR Parsing in C#: How to Use The Most Powerful Parsing Algorithm Known
Updated on 2020-02-18
A crash course in GLR parsing which can be used to parse highly ambiguous grammars
Introduction
This article aims to teach how to do Generalized LR parsing to parse highly ambiguous grammars. I've provided some experimental code which implements it. I wanted to avoid making the code complete and mature because that will involve adding a lot of complexity to it, and this way it's a bit easier to learn. There's not a lot of information on GLR parsing online so I'm entering this article and the associated code into the public domain. All I ask is you mention honey the codewitch (that's me!) in your project somewhere if you use it.
Conceptualizing this Mess
GLR stands for Generalized Left-to-right Rightmost derivation. The acronym is pretty clunky in its expanded form, but what it means essentially is that it processes ambiguous parses (generalized) from left to right, and bottom-to-top. Where did bottom-to-top come from? It's hinted at with Rightmost derivation.
Parsers that use the right-most form create right associative trees and work from the leaves to the root. That's a bit less intuitive than working from the root downward toward the leaves, but it's a much more powerful way to parse, and unlike top-to-bottom parsing, it can handle left recursion (and right recursion) whereas a left recursive grammar would cause a top-to-bottom parse to stack-overflow or otherwise run without halting, depending on the implementation details. Either way, that's not desirable. Parsing from the leaves and working toward the root avoids this problem as well as providing greater recognizing power. The tradeoff is it's much harder to create translation grammars for it which can turn one language into another, and it's generally a bit more awkward to use due to the counterintuitiveness of building the tree upward.
A Generalized LR parser works by using any standard LR parsing underneath. An LR parser is a type of Pushdown Automata which means it uses a stack and a state machine to do its processing. An LR parser itself is deterministic but our GLR parser is not. We'll square that circle in a bit. First we need to outline the single and fundamental difference between a standard LR parse table and GLR parse table. Don't worry if you don't understand the table yet. It's not important to understand the specifics yet.
A standard LR parser parsing table/state table looks like this:
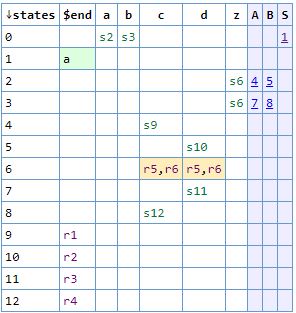
The above was generated using this tool.
It looks basically like a spreadsheet. Look at the cream colored cells though. See how there are two values? This causes an error with an LR parse table because it cannot hold two values per cell. The GLR parse table cells are arrays so they can hold multiple values. The above table, despite those cream colored conflicting cells, is perfectly acceptable to a GLR parser.
Any time there is a conflict like this, it's due to some localized or global ambiguity in the grammar. In other words, a grammar may not be ambiguous but if you're only looking ahead a little bit sometimes, it's not enough to disambiguate. It can be said that the production in the grammar is locally ambiguous. Otherwise, if the grammar is just generally ambiguous, then it's a globally ambiguity. Either way, this causes multiple values to be entered into the GLR table cell that handles that portion of the grammar.
No matter if it's local or global, an ambiguity causes the GLR parser to fork its stack and any other context information and try the parse each different way when presented with a multi-valued cell. If there is one value in the cell, no forking occurs. If there are two values, the parser forks its stack once. If there are three values, the parser forks its stack twice, and so on.
Since we're trying more than one path to parse, it can be said that our parser is non-deterministic. This impacts performance, and with a GLR parser performance is inversely proportional to how many forks are running. Additionally, each fork will result in a new parse tree. Note that this forking can be exponential in the case of highly ambiguous grammars. You pay the price for this ambiguity.
That's acceptable because GLR parsing was designed to parse natural/human language which can be highly ambiguous and the cost is baked in - to be expected in this case, and GLR is I believe still the most efficient generalized parsing algorithm to date since it only becomes non-deterministic if it needs to. As mentioned, rather than resolving to a single parse tree, a GLR parser will return every possible parse tree for an ambiguous parse, and again, that's how the ambiguity is handled whereas a standard LR parser will simply not accept an ambiguous grammar in the first place.
Generating the LR Parsing Table
We'll begin by addressing a fundamental task - creating those parse tables like the one above from a given grammar. You can't generate these by hand for anything non-trivial so don't bother trying. If you need a tool to check your work, try this. It takes a grammar in Yacc format and can produce a parse table using a variety of LR algorithms.
You may need to read this to understand rules, grammars and symbols. While it was written to teach about LL(1) parsers, the same concepts such as rules, symbols (non-terminal and terminal) and FIRST/FOLLOWS sets are also employed for this style of parsing. It's highly recommended that you read it because it gives all of the above a thorough treatment. Since it's enough to be an article in its own right, I've omitted it here.
Let's kick this off with an excellent resource on generating these tables, provided by Stephen Jackson here. We'll be following along as we generate our table. I used this tutorial to teach myself how to generate these tables, and it says they are LALR(1) but I've been told this is actually an SLR(1) algorithm. I don't know enough about either to be certain either way. Fortunately, it really doesn't matter because GLR can use any LR algorithm underneath. The only stipulation is that the less conflicts that crop up in the table, the more efficient the GLR parser will be. Less powerful algorithms create more conflicts. Because of this, while you can use LR(0) for a GLR parser, it would significantly degrade the performance of it due to all the local ambiguity. The code I've provided doesn't implement LR(0) because there was no good reason to.
Let's begin with the grammar from the tutorial part way down the page at the link:
- S → N
- N → V = E
- N → E
- E → V
- V → x
- V → * E
Generally, the first rule (0)/non-terminal S is created during the table generation process. We augment the grammar with it and point it to the actual start symbol which in this case would have been N, and then follow that with an end of input token (not shown)
That being said, we're going to overlook that and simply use the grammar as is. Note that the above grammar has its terminals as either lowercase letters like "x", or literal values like "=". We usually want to assign descriptive names to these terminals (like "equals") instead but this is fine here.
We need a data structure that's a lot like a rule with one important addition - an index property that indicates a position within the rule. For examine, we'd represent rule 0 from above using two of these structures like this:
S → • N
S → N •The bullet is a position within the rule. We'll each data structure an LR(0) Item, or LR0Item. The first one above indicates that N is the next symbol to be encountered, while the next one indicates that N was just encountered. We need to generate sets of these.
We start at the start rule, and create an LR0Item like the first one above, with the bullet before the N. Now since the bullet is before a non-terminal (N), we need to add each of the N rules, with a bullet at the beginning. Now our itemset (our set of LR0Items) looks like this:
S → • N
N → • V = E
N → • ESo far so good but we're not done yet as now we have two new LR0Items that have a bullet before a non-terminal (V and E, respectively) so we must repeat the above step for those two rules which means our itemset will now look like this:
S → • N
N → • V = E
N → • E
E → • V
V → • x
V → • * ENow our itemset is complete since the bullets are only before terminals or non-terminals that we've already added to the itemset. Since this is our first itemset, we'll call it itemset 0 or i0.
Now all we do to make the rest of the itemsets is apply each possible input** to the itemset and increment the cursor on the accepting rules. Don't worry, here's an example:
We start by giving it x. There's only one entry in the itemset that will accept it next and that is the second to last LR0Item - V → • x so we're going to create our next itemset i1 with the result of that move:
*_ We don't need to actually pass it each input. We only need to look at the next terminals already in the itemset. For i0 the next terminals are _ and x. Those are the inputs we use.
V → x •That is the single entry for i1. Now we have to go back to i0 and this time move on * which yields:
V → * • EThat is our single entry for itemset i2 so far but we're not done with it. Like before, a bullet is before a non-terminal E, so we need to add all the rules that start with E. There's only one in this case, E → • V which leaves us with this itemset so far:
V → * • E
E → • VNote that when we're adding new items, the cursor is at the start. Once again, we have a bullet before a non-terminal in the rule E → • V so we have to add all the V rules, which leaves is with our final itemset for i2:
V → * • E
E → • V
V → • x
V → • * ELook, we encountered our V → • x and V → • * E and items from i0 again! This can happen and it's supposed to. They were added because of E → • V. Now we're done since the cursor is only before terminals or non-terminals that have already been added.
Now we need to move on i0 again, this time on the non-terminal V. Moving on V yields the following itemset i3:
N → V • = E
E → V •One additional difficulty of generating these itemsets is duplicates. Duplicate itemsets must be detected, and they must not be repeated.
Anyway, here are the rest of the itemsets in case you get stuck:
i4:
S → N •i5:
N → E •i6:
V → * E •i7:
E → V •i8:
N → V = • E
E → • V
V → • x
V → • * Ei9:
N → V = E •Generating these is kind of tricky, perhaps moreso than it seems and I haven't laid out all we need to do above yet. While you're building these itemsets, you'll need to create some kind of transition map between the itemsets. For example, on i0 we can transition to i1 on x and to i2 on *. We know this because we worked it out while we were creating our i0 itemset. Stephen Jackson's tutorial has it laid out as a separate step but for expediency we want to roll it into our steps above. It makes things both easier and more efficient. Remember to detect and collate duplicate sets.
Now, I'll let you in on something I've held back up until now: Each itemset above represents a state in a state machine, and the above transitions are transitions between the states. We have 10 states for the above grammar, i0 through i9. Here's how I store and present the above data, as a state machine:
sealed class LRFA
{
public HashSet<LR0Item> ItemSet = new HashSet<LR0Item>();
public Dictionary<string, LRFA> Transitions = new Dictionary<string, LRFA>();
// find every state reachable from this state, including itself (all descendants and self)
public ICollection<LRFA> FillClosure(ICollection<LRFA> result = null)
{
if (null == result)
result = new HashSet<LRFA>();
if (result.Contains(this))
return result;
result.Add(this);
foreach(var trns in Transitions)
trns.Value.FillClosure(result);
return result;
}
}Basically, this allows you to store the computed transitions along with the itemset. The dictionary maps symbols to LRFA states. The name is ugly but it stands for LR Finite Automata, and each LRFA instance represents a single state in a finite state machine. Now that we have it we're going to pull a fast one on our algorithm, and rather than running the state machine, we're going to walk through it and create a new grammar with the state transitions embedded in it. That's our next step.
The state numbers are different below than the demonstration above out of necessity. I wanted you to be able to follow the associated tutorial at the link, but the following was generated programmatically and I don't control the order the states get created in.
For this next step, we'll be walking through the state machine we just created following each transition. Start at i0. Here we're going from i0 to each transition, through the start symbol, to the end of the input as signified by $ in the below grammar, so first we write 0/S/$ as the rule's left hand side which signifies i0, the start symbol S and the special case end of input $ as there is no actual itemset for that. From there, we only have one transition to follow, on N which leads us to i1, so we write as the single right hand side 0/N/1 leaving us with:
0/S/$ → 0/N/1Those are some ugly symbol names, but it doesn't matter, because the computer loves them, I swear. Truthfully, we need these for a couple of reasons. One, this will disambiguate transitions from rule to rule because now we have new rules for each transition possibility, and two we can use it later to get some lookahead into the table, which we'll get into.
Next we have to follow N so we do that, and repeat. Notice how we've create two rules with the same left hand here. That's because we have two transitions.
0/N/1 → 0/V/2 2/=/3 3/E/4
0/N/1 → 0/E/9We only have to do this where LR0Items are at index 0. Here's what we're after:
0/S/$ → 0/N/1
0/N/1 → 0/V/2 2/=/3 3/E/4
0/N/1 → 0/E/9
0/V/2 → 0/x/6
0/V/2 → 0/*/7 7/E/8
0/E/9 → 0/V/2
3/E/4 → 3/V/5
3/V/5 → 3/x/6
3/V/5 → 3/*/7 7/E/8
7/E/8 → 7/V/5
7/V/5 → 7/x/6
7/V/5 → 7/*/7 7/E/8Finally, we can begin making our parse table. These are often sparse enough that using a dictionary is warranted, although a matrix of nested arrays works too as long as you have a little more memory.
An LR parser has four actions it can perform: shift, reduce, goto and accept. The first two are primary operations and it's why LR parsers are often called shift-reduce parsers.
The parse table creation isn't as simple as it is for LL(1) parsers, but we've come pretty far. Now if you're using a dictionary and string symbols you'll want a structure like Dictionary<string,(int RuleOrStateId, string Left, string[] Right)>[] for a straight LR parse table or Dictionary<string,ICollection<(int RuleOrStateId, string Left, string[] Right)>>[] for a GLR parse table.
That's right, an array of dictionaries with a tuple in them, or in GLR's case, an array of dictionaries with a collection of tuples in them.
Now the alternative, using integer symbol ids can be expressed as int[][][] for straight LR or int[][][][] for GLR. Despite the efficiency, so many nests are confusing and it's best to use this form for generated parsers. You can create these arrays from a dictionary based parse table anyway. Below we'll be using the dictionary form.
Initialize the parse table array with one element for each state. Above we had 10 states, so our declaration would look like new Dictionary<string,(int RuleOrStateId, string Left, string[] Right)>[10].
Next compute the closure of our state machine we built earlier as a List
Create a list of itemsets (List<ICollection
Now for each LRFA in the closure, treat its index in the closure as an index into your parse table's dictionaries array. The first thing you do is create the dictionary for that array entry.
Then go through each of the transitions in that LRFA. For any symbol, use that as a dictionary key. This will be a "shift" operation in the case of a terminal and a "goto" operation if it's a non-terminal. To create tuple for a shift or goto operation set RuleOrStateId to the index of the transition's destination state. You can find this index by using IndexOf() over the closure list.
Now while you're on that LRFA in the loop, scan its itemset looking for an LR0Item that has the Index at the very end and where the left hand of the associated rule is the start symbol, and if you find it add an entry to the parse table in that associated state's dictionary, key of the end symbol ($) and value of a tuple with RuleOrStateId of -1 and both Left and Right set to null. This indicates an "accept" action.
Now we need to fill in the reductions. This can be sort of complicated. Remember our extended grammar? It's time to use it. First, we take the FOLLOW sets for that grammar. This is non-trivial and lengthy to describe so I'm punting the details of doing it to this article I linked you to early on. The project contains a FillFollows() function that will compute the follows set for you.
Now that you have them, you'll need to map each extended rule in the grammar to the follows for its left hand side. I use a dictionary for this, like Dictionary<CfgRule,ICollection
Note: In the case of epsilon/nil rules like A →, you'll need to handle them slightly differently below.
Now for each entry in your above map dictionary, you'll need to do the following:
Take the rule and its final number** - the final number is the index into your array of dictionaries that makes up your parse table, (remember that thing still?) For each entry entry in the FOLLOW items in your map entry's Value, add a tuple to the parse table. To create the tuple for this, simply strip the rule to its unextended form, find the index of the rule within the grammar, and then use that, along with the left and right hand side of the rule in the corresponding spots in the tuple. For example, if rule at index 1 is N → V = E then the tuple would be (RuleOrStateId: 1, "N" , new string[] { "V", "=", "E" }). Now, check to see if the dictionary already has an entry for this FOLLOW symbol. If it does, and it's the same, no problem. That may happen, but it's fine. If it does and it's not the same, this is a conflict. If the existing tuple indicates a shift, this is shift-reduce conflict. This isn't a parse killer. Sometimes, these are unavoidable such as the dangling else in C family languages. Usually, the shift will take precedence. If the existing tuple indicates a reduce action, this is a reduce-reduce conflict. This will stop a standard LR parser dead in its tracks. With a GLR parser, both alternatives will be parsed. Anyway, if this a GLR table and a tuple is already present, just add another tuple. If it's a regular LR parser, and it was a shift just pick an action (usually the shift) to take priority, and ideally issue a warning about the conflict to the user, but not with GLR. If the previous tuple is a reduce, issue an error, but not with GLR.
** For epsilon/nil rules, you'll need to take the final number from the left hand side of the rule.
We did it! That's a lot of work but now have a usable parse table. For production code, you may want to have some sort of progress indicator because this operation can take some significant time for real world grammars.
Parsing With Standard LR(1)
No matter the algorithm, be it LALR(1), SLR(1) or full LR(1) the parse tables are the same in overall structure. The GLR parse table contains one important difference in that the cells are arrays.
Because of this for LR, our parse code is the same regardless of the algorithm (excepting GLR). However, since GLR uses these principles to parse we will cover standard LR parsing here.
Parsing with LR is somewhat convoluted but overall simple once you get past some of the twists involved.
You'll need the parse table, a stack and a tokenizer. The tokenizer will give you tokens with symbols, values, and usually line/position info. If the tokenizer reports only symbol ids, you'll need to do a lookup to get the symbol, so you'll need at least an array of strings as well.
The parse table will direct the parser and use of the stack and input using the following directives:
- Shift: Indicated by a tuple of (#,null,null) (where # is an index) in our parse table.
- Push the index, #, onto the stack.
- Read the next token in the input and stash it.
- Reduce: Indicated by (#,left,right) (where # is the rule id, and left and right are the rule symbols) in our parse table
- Report the rule to the output.
- Get the number of tokens on the right-hand side of rule and pop the stack that many times.
- Now, the number at the top of the stack indicates a new state. Get the symbol from the left-hand side of the rule and consult the parse table at the new state using the left-hand side as an input token in the dictionary. Push the value you just got on top of the stack.
- Accept: Indicated by (-1,null,null). Accepted the parse and finished.
If no entry is found, this is a syntax error.
Let's revisit Stephen Jackson's great work:
Let's walk through the first steps in parsing x = * x. The first step is to initialize the stack and read the first token, basically pushing 0 onto the stack
Input Output Stack Next x = * x$ 0 Shift 1
The first token we found in state 0 was an x, which indicates that we must shift to state 1. 1 is placed on the stack and we advance to the next token. That leads us to the following:
Input Output Stack Next x = * x$ 0 Shift 1 = * x$ 0, 1 Reduce 4
When we reduce, we report the rule for the reduction. Rule 4, V → x, has 1 token (x) on the right-hand side. Pop the stack once, leaving it with 0. In state 0, V (the left-hand side of rule 4) has a goto value of 3, so we push a 3 on the stack. This step gives us our table a new row:
Input Output Stack Next x = * x$ 0 Shift 1 = * x$ 0, 1 Reduce 4 = * x$ 4 0, 3 Shift 8
Here's the whole process:
Input Output Stack Next x = * x$ 0 Shift 1 = * x$ 0, 1 Reduce 4 = * x$ 4 0, 3 Shift 8 * x$ 4 0, 3, 8 Shift 2 x$ 4 0, 3, 8, 2 Shift 1 $ 4 0, 3, 8, 2, 1 Reduce 4 $ 4, 4 0, 3, 8, 2, 7 Reduce 3 $ 4, 4, 3 0, 3, 8, 2, 6 Reduce 5 $ 4, 4, 3, 5 0, 3, 8, 7 Reduce 3 $ 4, 4, 3, 5, 3 0, 3, 8, 9 Reduce 1 $ 4, 4, 3, 5, 3, 1 0, 4 Accept
By itself, that doesn't look very useful but we can easily build trees with that information. Here, Stephen Jackson explains the results:
Stephen Jackson writes:
In our example of x = * x we get the output 4, 4, 3, 5, 3, 1. To review, we'll construct objects based on the example.
When the first reduction occurred (r4) we had just inputted the terminal x. By rule 4, V → x, x mapped onto the non-terminal V. Thus we have our first object, V(x).
The second time a reduction occurs (r4) is just after we've inputted the entire string meaning that we are turning the last x into a V. Which gives us our second object, V(x). At this point we can re-substitute our objects back into the string, which gives us V(x) = * V(x).
Reduction 3 just maps the last V(x) into E(V(x)). Giving us V(x) = * E(V(x)).
The remaining mappings are:
- V(x) = V(* E(V(x)))
- V(x) = E(V( * E(V(x))))
- N(V(x) = E(V( * E(V(x)))))
- S(N(V(x) = E(V( * E(V(x))))))
It is a cumbersome way of looking at it. But it shows how to map the LR parsing method into constructors. And if we give each rule a function, then it should be obvious how to generate code. For example, V(x) could be used to make token x into an object of type V. Any object of type E is formed by giving the constructor an object of type V. And so on until we reach the eventual end of this example by creating an object of type S by giving it an object of type N.
Parsing With GLR
Naturally, parsing with GLR is a bit more complicated than the above, but it is at least based on the same principles. With GLR, it's best to make an overarching parser class, and then delegate the actual parsing to a worker class. This way, you can run several parses concurrently by spawning multiple workers, which is what we need. Each worker manages its own stack, an input cursor and any other state.
The complication is not really in running the workers like one might think but rather managing the input token stream. The issue is that each worker might be in a slightly different position than the next even if we run them in lockstep so what we must do is create a sliding window to manage the input. The window should expand as necessary (when the workers get further apart from each other in the input) and shrink when possible (such as when a worker is removed or the workers move closer together.) I use my LookAheadEnumerator
The only issue for huge documents is you may want to use the pull parser directly rather than generating a tree, which could take an enormous amount of memory. The pull parser can be a little tricky to use, because while it works a bit like XmlReader, it also reads concurrently from different parses, meaning you'll have to check the TreeId every time after you Read() to see which "tree" you're currently working on.
Anyway, in implementing this, we use the parse table exactly like before except when we encounter multiple tuples in the same cell. When we find more than one we must "fork" a new worker for each additional tuple which gets its own copy of the stack and its own independent input cursor (via LookAheadEnumerator
There's a wrinkle in generating the parse trees that's related to the fact that we parse multiple trees at the same time. When the parser forks a worker (as indicated by the presence of a new TreeId that hasn't been seen yet we must (similarly to the parsing itself) clone the tree stack to accommodate it. Basically, we might be happily parsing along with worker TreeId of 1, having already built a partial tree when all of the sudden we fork and start seeing TreeId 2. When that happens, we must clone the tree stack from #1 and then continue, adding to each tree stack as appropriate. Finally, each tree id that ends up accepting winds up being a parse tree we return.
Coding this Mess
I have not provided you a parser generator, but simply an experimental parser and the facilities to define a grammar and produce a parser from it. A parser generator would work the same way except that the arrays we initialize the parser with would have been produced from generated code. That makes things just a little easier.
All of the directly relevant code is under namespace C. The other namespaces provide supporting code that isn't directly related to what we've done so far above. You'll see things like LexContext.cs in the project which exposes a text cursor as a LexContext class under namespace LC. We use that to help parse our CFG files, which we'll get to very soon, but it isn't related to the table building or parsing we were exploring above, as CFG documents are trivial and parsed with a hand rolled parser. CFG document here, means Context Free Grammar document. This is a bit of a misnomer with GLR since GLR can technically parse from a contextful grammar as well, but it still has all the properties of a regular CFG so the name is fine, in fact it's still preferable as all of the mathematical properties that apply to CFGs apply here too.
exposes a text cursor as a LexContext class
Open the solution and navigate to the project "scratch" in your IDE. This is our playground for twiddling with the parser.
Let's try it now. Create a new CFG document. Since I like JSON for examples, let's define one for JSON which we'll name json.cfg:
(This document is provided for you with the project to save you some typing.)
json -> object | array
object -> lbrace rbrace | lbrace fields rbrace
fields -> field | field comma fields
field -> string colon value
array -> lbracket rbracket | lbracket values rbracket
values -> value | value comma values
value -> string | number | object | array | boolean | null
boolean -> true | falseGreat, but now what? First, we need to load this into a CfgDocument class:
var cfg = CfgDocument.ReadFrom(@"..\..\json.cfg");
cfg.RebuildCache(); // not necessary, but recommendedThe second line isn't necessary but it's strongly recommended especially when dealing with large grammars. Any time you change the grammar, you'll need to rebuild the cache. Since we don't intend to change it, just to load it and generate tables from that means we can cache it now.
There's also a Parse() function and a ReadFromUrl() function. ToString() fulfills the correlating conversion back into the above format (except longhand, without using | ) while an overload of it can take "y" as a parameter which causes it to generate the grammar in Yacc format for use with tools like the JISON visualizer I've linked to prior.
A CfgDocument is made up of Rules as represented by CfgRule. In the above scenario, we loaded these rules from a file but you can add, remove and modify them yourself. The rule has a left hand and right hand side which are composed of symbols. Meanwhile, each symbol is represented by a string, with the reserved terminal symbols #EOS and #ERROR being automatically produced by CfgDocument. Use the document to query for terminals, non-terminals and rules. You can also use it to create FIRST, FOLLOW, and PREDICT sets. All of these are accessed using the corresponding FillXXXX() functions. If you remember, we use the FOLLOW sets to make our LR and GLR parse tables above. This is where we got them from, except our CFG was an extended grammar rules like 0/S/$ -> 0/N/1 as seen before.
This is all well and good, but what about what we're actually after? - parse tables! Remember that big long explanation on how to generate them? I've provided all of that in CfgDocument.LR.cs which provides TryToLR1ParseTable() and TryToGlrParseTable(). The former function doesn't generate true LR(1) tables because those would be huge. Instead, it takes a parameter which tells us what kind of LR(1) family of table we want. Currently the only option is Lalr1 for LALR(1), but that suits us just fine. TryToGlrParseTable() will give us the GLR table we need.
Each of these functions returns a list of CfgMessage objects which can be use to report any warnings or errors that crop up. There won't be any for GLR table creation since even conflicting cells (ambiguous grammars) are valid, but I've provided it just the same for consistency. Enumerate through the messages and report them or simply pass them to CfgException.ThrowIfErrors() to throw if any of the messages were ErrorLevel.Error. The out value gives us our CfgLR1ParseTable or our CfgGlrParseTable, respectively. Now that we have those, we have almost enough information to create a parser.
One thing we'll need in order to parse is some sort of implementation of IEnumerable
On to the simpler things. One is the symbol table which we can get by simply calling FillSymbols() and converting that to a string[]. The other is the error sentinels (int[]) which will require some explanation. In the case of an error, the parsers will endeavor to keep on parsing so that all errors can be found in a single pass. This is easier said than done. We use a simple technique called "panic mode" error recovery that is a form of local error recovery. This requires that we define a safe ending point for when we encounter an error. For languages like C, this can mean ;/semi and }/rbrace which is very reasonable. For JSON, we'll use ]/rbracket, ,/comma and }/rbrace. When an error happens, we gather input tokens until we find one of those, and then pop the stack until we find a valid state for a sentinel or run out of states to pop. Ideally, we'd only use this method for a standard LR parser, and use a form of global error recovery for the GLR parser. However, the latter is non-trivial and not implemented here, even though it would result in better error handling. Our errorSentinels array will contain the indices into the symbol table for our two terminals.
Finally, we can create a parser. Here's the whole mess from beginning to end:
var cfg = CfgDocument.ReadFrom(@"..\..\json.cfg");
cfg.RebuildCache();
// write our grammar out in YACC format
Console.WriteLine(cfg.ToString("y"));
// create a GLR parse table. We can use a standard LR parse table here.
// We're simply demoing the GLR parser
CfgGlrParseTable pt;
var msgs = cfg.TryToGlrParseTable(out pt);
// there shouldn't be any messages for GLR, but this is how we process them if there were
foreach(var msg in msgs)
Console.Error.WriteLine(msg);
CfgException.ThrowIfErrors(msgs);
// create the symbol table to map symbols to indices which we treat as ids.
var syms = new List<string>();
cfg.FillSymbols(syms);
// our parsers don't use the parse table directly.
// they use nested arrays that represent it for efficiency.
// we convert it using ToArray() passing it our symbol table
var pta= pt.ToArray(syms);
// now create our error sentinels. If this is an empty array only #EOS will be considered
var errorSentinels = new int[] { syms.IndexOf("rbracket"), syms.IndexOf("rbrace") };
// let's get our input
string input;
using (var sr = new StreamReader(@"..\..\data2.json"))
input = sr.ReadToEnd();
// now make a tokenizer with it
var tokenizer = new JsonTokenizer(input);
var parser = new GlrTableParser(pta, syms.ToArray(), errorSentinels,tokenizer);
// uncomment the following to display the raw pull parser output
/*
while(parser.Read())
{
Console.WriteLine("#{0}\t{1}: {2} - {3}",
parser.TreeId, parser.NodeType, parser.Symbol, parser.Value);
}
// reset the parser and tokenizer
tokenizer = new JsonTokenizer(input);
parser = new GlrTableParser(pta, syms.ToArray(), errorSentinels,tokenizer);
*/
Console.WriteLine();
Console.WriteLine("Parsing...");
Console.WriteLine();
// now for each tree returned, dump it to the console
// there will only be one unless the grammar is ambiguous
foreach(var pn in parser.ParseReductions())
Console.WriteLine(pn);To try with different grammars, simply switch out the grammar filename, the error sentinels, the tokenizer and the input. Test14.cfg is a small ambiguous grammar that can be used to test. I recommend it with an input string like bzc.
Anyway, for the JSON grammar and the associated input, we get:
%token lbrace rbrace comma string colon lbracket rbracket number null true false
%%
json : object
| array;
object : lbrace rbrace
| lbrace fields rbrace;
fields : field
| field comma fields;
field : string colon value;
array : lbracket rbracket
| lbracket values rbracket;
values : value
| value comma values;
value : string
| number
| object
| array
| boolean
| null;
boolean : true
| false;
Parsing...
+- json
+- object
+- lbrace {
+- fields
| +- field
| +- string "backdrop_path"
| +- colon :
| +- value
| +- string "/lgTB0XOd4UFixecZgwWrsR69AxY.jpg"
+- rbrace }Meanwhile, doing it for Test14 as suggested above yields two parse trees:
%token a c d b z
%%
S : a A c
| a B d
| b A d
| b B c;
A : z;
B : z;
Parsing...
+- A
+- b b
+- A
| +- z z
+- #ERROR c
+- S
+- b b
+- B
| +- A
| +- z z
+- c cThe first one was no good as it tried the wrong reduce - or rather, that reduce didn't pan out this time but it theoretically may have with the right grammar and given a different input string. You'll note the error recovery is still poor, and this is still a work in progress. I'm experimenting with different techniques to improve it so that it will continue without clearing the stack in so many cases. In any case, our second tree resulted in a valid parse. With some grammars, multiple trees may be valid and error free due to ambiguity. For some inputs, every tree might have errors, but the errors might be different in each one. Figuring out which tree to pick is not the GLR parsers job. It depends heavily on what you intend to do with it. With C# for example, you might get many different trees due to the ambiguity of the language, but applying type information can narrow the trees down to the single valid tree the code represents.
The Gory Details
GlrTableParser delegates to GlrWorker which implements an LR(1) parser in its own right. We spawn one of these workers for each path through the parse. Only the first one is created by GlrTableParser itself. The workers create themselves after that during the parse. At each fork, we create a new one for each alternate path which can yield exponential GlrWorker creation in highly ambiguous grammars, so make your grammars tight to get the best performance. We know we've encountered a fork when there are multiple entries in the parse table cell at our current state and position. Here, we see the lookup in the parse table in GlrWorker.Read(). Note the code in bold, and how it spawns more workers for every tuple after the first one.
public bool Read()
{
if(0!=_errorTokens.Count)
{
var tok = _errorTokens.Dequeue();
tok.SymbolId = _errorId;
CurrentToken = tok;
return true;
}
if (_continuation)
_continuation = false;
else
{
switch (NodeType)
{
case LRNodeType.Shift:
_ReadNextToken();
break;
case LRNodeType.Initial:
_stack.Push(0);
_ReadNextToken();
NodeType = LRNodeType.Error;
break;
case LRNodeType.EndDocument:
return false;
case LRNodeType.Accept:
NodeType = LRNodeType.EndDocument;
_stack.Clear();
return true;
}
}
if (0 < _stack.Count)
{
var entry = _parseTable[_stack.Peek()];
if (_errorId == CurrentToken.SymbolId)
{
_tupleIndex = 0;
_Panic();
return true;
}
var tbl = entry[CurrentToken.SymbolId];
if(null==tbl)
{
_tupleIndex = 0;
_Panic();
return true;
}
int[] trns = tbl[_tupleIndex];
// only create more if we're on the first index
// that way we won't create spurious workers
if (0 == _tupleIndex)
{
for (var i = 1; i < tbl.Length; ++i)
{
_workers.Add(new GlrWorker(_Outer, this, i));
}
}
if (null == trns)
{
_Panic();
_tupleIndex = 0;
return true;
}
if (1 == trns.Length)
{
if (-1 != trns[0]) // shift
{
NodeType = LRNodeType.Shift;
_stack.Push(trns[0]);
_tupleIndex = 0;
return true;
}
else
{ // accept
//throw if _tok is not $ (end)
if (_eosId != CurrentToken.SymbolId)
{
_Panic();
_tupleIndex = 0;
return true;
}
NodeType = LRNodeType.Accept;
_stack.Clear();
_tupleIndex = 0;
return true;
}
}
else // reduce
{
RuleDefinition = new int[trns.Length - 1];
for (var i = 1; i < trns.Length; i++)
RuleDefinition[i - 1] = trns[i];
for (int i = 2; i < trns.Length; ++i)
_stack.Pop();
// There is a new number at the top of the stack.
// This number is our temporary state. Get the symbol
// from the left-hand side of the rule #. Treat it as
// the next input token in the GOTO table (and place
// the matching state at the top of the set stack).
// - Stephen Jackson, https://web.cs.dal.ca/~sjackson/lalr1.html
var state = _stack.Peek();
var e = _parseTable[state];
if (null == e)
{
_Panic();
_tupleIndex = 0;
return true;
}
_stack.Push(_parseTable[state][trns[1]][0][0]);
NodeType = LRNodeType.Reduce;
_tupleIndex = 0;
return true;
}
}
else
{
// if we already encountered an error
// return EndDocument in this case, since the
// stack is empty there's nothing to do
NodeType = LRNodeType.EndDocument;
_tupleIndex = 0;
return true;
}
}Refer to the tutorial on running a parse given earlier. See how we initially grab the tuple given by _tupleIndex and then reset it to zero? That's because we only want to take the alternate path once. The worker only takes an alternate path the first time it is Read() and after that, it spawns additional workers for each of the alternate paths it encounters, wherein they revert to the first path after the inital Read() as well, and spawn more workers for any alternates they encounter and so on. Yes, again, this can yield exponential workers. It's the nature of the algorithm. Walking each possible path requires exponential numbers of visits for each choice that can be made.
Also note how we report the rule definition used during a reduction. This is critical so that the user of the parser can match terminals back to the rules they came from. It's simply stored as int[] where index zero is the left hand side's symbol id, and the remainder are the ids for the right hand symbols.
Another issue is in creating a new worker from an existing worker. We must copy its stack and other state and receive an independent input cursor and a tuple index to tell us which path to take on the initial read. On the initial read, we skip the first part of the routine which is what _continuation is for - we're restarting the parse from where we left off. Here's the constructor for the worker that takes an existing worker:
public GlrWorker(GlrTableParser outer,GlrWorker worker,int tupleIndex)
{
_Outer = outer;
_parseTable = worker._parseTable;
_errorId = worker._errorId;
_eosId = worker._eosId;
_errorSentinels = worker._errorSentinels;
ErrorTokens = new Queue<Token>(worker.ErrorTokens);
_tokenEnum = worker._tokenEnum;
var l = new List<int>(worker._stack);
l.Reverse();
_stack = new Stack<int>(l) ;
Index = worker.Index;
_tupleIndex = tupleIndex;
NodeType = worker.NodeType;
Id = outer.NextWorkerId;
CurrentToken = worker.CurrentToken;
unchecked { ++outer.NextWorkerId; }
_continuation = true;
_workers = worker._workers;
}Here, we create our new worker, using a somewhat awkward but necessary way to the clone the stack - I really should use my own stack implementation to solve this but I haven't for this code. We assign a new id to the worker, we indicate that it's a continuation, copy our parse table and error sentinel references and create a queue to hold errors we need to report. It's not shown here but _Outer is actually a property that wraps _outer, itself a WeakReference
That covers the meat of our worker class. Let's cover the GlrTableParser that delegates to it. Mainly, we're concerned with the Read() method which does much of the work:
public bool Read()
{
if (0 == _workers.Count)
return false;
_workerIndex = (_workerIndex + 1) % _workers.Count;
_worker = _workers[_workerIndex];
while(!_worker.Read())
{
_workers.RemoveAt(_workerIndex);
if (_workerIndex == _workers.Count)
_workerIndex = 0;
if (0 == _workers.Count)
return false;
_worker = _workers[_workerIndex];
}
var min = int.MaxValue;
for(int ic=_workers.Count,i=0;i<ic;++i)
{
var w = _workers[i];
if(0<i && w.ErrorCount>_maxErrorCount)
{
_workers.RemoveAt(i);
--i;
--ic;
}
if(min>w.Index)
{
min=w.Index;
}
if (0 == min)
break;
}
var j = min;
while(j>0)
{
_tokenEnum.MoveNext();
--j;
}
for (int ic = _workers.Count, i = 0; i < ic; ++i)
{
var w = _workers[i];
w.Index -= min;
}
return true;
}Here if we don't have any workers, we're done. Then we increment the _workerIndex, round-robin like and use that to choose the current worker we delegate to among all the current workers. For each worker, starting at the _workerIndex, we try to Read() from the next worker, and if it returns false then we remove it from the _workers and try the next worker. We continue this process until we find a worker that read or we run out of workers. If we're out of workers we return false.
Now, after a successful Read(), we check all the workers for how much they've advanced along the current primary cursor by checking their Index. We do this for all the workers because some may not have been moved forward during the last Read() call. Anyway, the minimum advance is what we want to slide our window by, so we increment the primary cursor by that many. Next, we fix all of the workers Indexes by subtracting that minimum value from them. Finally, we return true to indicate a successful read.
One more thing of interest about the parser is the ParseReductions() method which will return trees from the reader. The trees of course, are much easier to work with then the raw reports from the pull parser. Here's the method:
public ParseNode[] ParseReductions(bool trim = false, bool transform = true)
{
var map = new Dictionary<int, Stack<ParseNode>>();
var oldId = 0;
while (Read())
{
Stack<ParseNode> rs;
// if this a new TreeId we haven't seen
if (!map.TryGetValue(TreeId,out rs))
{
// if it's not the first id
if (0 != oldId)
{
// clone the stack
var l = new List<ParseNode>(map[oldId]);
l.Reverse();
rs = new Stack<ParseNode>(l);
}
else // otherwise create a new stack
rs = new Stack<ParseNode>();
// add the tree id to the map
map.Add(TreeId, rs);
}
ParseNode p;
switch (NodeType)
{
case LRNodeType.Shift:
p = new ParseNode();
p.SetLocation(Line, Column, Position);
p.Symbol = Symbol;
p.SymbolId = SymbolId;
p.Value = Value;
rs.Push(p);
break;
case LRNodeType.Reduce:
if (!trim || 2 != RuleDefinition.Length)
{
p = new ParseNode();
p.Symbol = Symbol;
p.SymbolId = SymbolId;
for (var i = 1; RuleDefinition.Length > i; i++)
{
var pc = rs.Pop();
_AddChildren(pc, transform, p.Children);
if ("#ERROR" == pc.Symbol)
break;
}
rs.Push(p);
}
break;
case LRNodeType.Accept:
break;
case LRNodeType.Error:
p = new ParseNode();
p.SetLocation(Line, Column, Position);
p.Symbol = Symbol;
p.SymbolId = _errorId;
p.Value = Value;
rs.Push(p);
break;
}
oldId = TreeId;
}
var result = new List<ParseNode>(map.Count);
foreach (var rs in map.Values)
{
if (0 != rs.Count)
{
var n = rs.Pop();
while ("#ERROR" != n.Symbol && 0 < rs.Count)
_AddChildren(rs.Pop(), transform, n.Children);
result.Add(n);
}
}
return result.ToArray();
}This is just an iterative way of interpreting the parse results as Stephen Jackson covered above, except his was recursive and was only dealing with one parse tree. It would be very difficult, if not impossible to implement this recursively given that different tree information can be returned in any order.
Stay tuned for GLoRy, a parser generator that takes this code to the next level to generate parsers for virtually anything parseable.
History
- 18th February, 2020 - Initial submission