How to Build a Regex Engine in C#
Updated on 2019-11-21
Build a feature rich, non-backtracking regular expression engine and code generator in C#
Update:
See my Unicode enabled offering here
Prerequisites
The project solution is in Visual Studio 2017 format. It's compiled as a standard library and a Core executable.
Furthermore, in order to get rendering support, you'll need to install GraphViz which this code uses to render state graphs into images. All you should have to do is run the installer for GraphViz, and it should be in your path. You do not need GraphViz for using most of the regex functionality. You only need it to make pretty pictures, like the images in this article.
Since we're using .NET Standard and .NET Core, we also reference the Code DOM NuGet package. This is necessary for the code generation facilities.
Introduction
This is an ambitious article. The goal is to walk you through the building of a fully featured regular expression engine and code generator. The code contains a complete and ready to use regular expression engine, with plenty of comments and factoring to help you through the source code.
First of all, you might be wondering why we would develop one in the first place. Aside from the joy of learning how regular expressions work under the hood, there's also a gap in the .NET framework's regular expression classes which this project fills nicely. This will be explained in the next section.
I've previously written a regular expression engine for C# which was published here, but I did not explain the mechanics of the code. I just went over a few of the basic principles. Here, I aim to drill down into a newer, heavily partitioned library that should demystify the beast enough that you can develop your own or extend it.
I didn't skimp on optimizations, despite the added complication in the source. I wanted you to have something you could potentially use "out of the box." That said, providing you with the end library is a secondary goal. The primary goal is to teach you how to build one yourself.
Conceptualizing this Mess
This article assumes passing familiarity with common regular expression notation. You don't have to be an expert, but knowing what ?, *, +, |, [], and () do is very helpful. If you only know a subset, that's okay too, as long as you understand the basic idea behind regular expressions and what they're for.
What you might not know, is the theory behind their operation, which we'll cover here.
At its core, a regular expression is a finite state machine based on a directed graph. That is to say, it is a network of nodes, connected to other nodes along directional paths. This is easier to visualize than to describe:
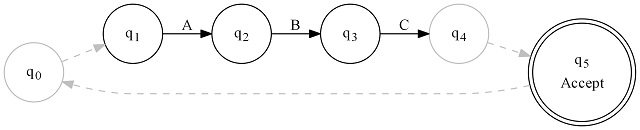
finite state machine directed graph
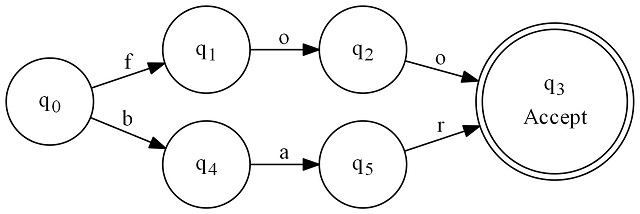
This regular expression graph matches "foo" or "bar". The regular expression for this would be foo|bar.
Here's how it works: We always start at q0. From there, we have a series of black arrows pointing away. Each one is labeled with a character. Well, we examine the first character of the string to match. If it is "f" we proceed to q1. If it is "b" we proceed to q4. Any time we move along a black arrow, we increment the input string's cursor position by one. On q1 or q4, we will be examining the next input character, and so on. This continues until we can no longer match any characters. If at that point, we are on a state with a double circle (an "accepting state"), we have matched. If we are on some single circle state at that point, then we have not matched.
We can create these graphs based on parsing a regular expression, and then use code to "run" these graphs, such that they can match input strings.
Speaking of matching, there are two significantly different ways to use a regular expression engine. The first, and perhaps the most common is to scan through a long string of text looking for certain patterns. This is what you do in the Search and Replace dialog in Visual Studio if you enable regular expression matching for example. This is well covered ground for Microsoft's regular expression engine, and it is generally best practice to use it in these cases. For long strings, it can outperform our library since it implements things like Boyer-Moore searches whereas ours does not. Generally, it's a good idea to rely on Microsoft's engine for this style of matching.
The other way to use a regular expression engine is called tokenizing. This basically moves through an input stream, and it attempts to match a string under the cursor to a particular pattern, and then it reports the pattern that was matched, before advancing. Basically, it uses a compound regular expression (combined with ors) and matches text to one of the particular expressions - and tells you which one it was that matched. This is very useful for lexers/tokenizers which are used by parsers. Microsoft's regular expression engine is not suited to this task, and attempts to use it for this come with a number of disadvantages including additional code complexity and a considerable performance hit. This gap in functionality is enough to justify a custom regular expression engine if one is crafting parsers or tokenizing for some other reason.
Unlike Microsoft's regular expression engine, this engine does not backtrack. That is, it will never examine a character more than once. This leads to better performance, but non-backtracking expressions aren't quite as expressive/powerful as backtracking ones. Things like atomic zero width assertions are not possible using this engine, but the trade-off is more than worth it, especially when used for tokenizing.
Returning to the graphs, as alluded to, each one of these represents a finite state machine. The state machine has a root always represented by q0. If we were to take any subset of the graph, like, say starting at q4 and ignoring anything not pointed to directly or indirectly by q4, then that is also a state machine. Basically, a finite state machine is a set of interconnected state machines!
To find your entire state machine from the node you're presently on, you take the closure of a state. The closure is the set of all states reachable directly or indirectly from some state, including itself. The closure for q0 is always the entire graph. In this case, the closure for q4 is { q4, q5, q3 }. Note we never move backward along an arrow. The graph is directed. Taking the closure is a core operation of most any finite state machine code.
Let's move on to a slightly more complicated example: (foo|bar)+. Basically, we're just adding a loop to the machine so it can match "foobarfoo" or "foofoobar" or "barbarfoofoobar", etc.
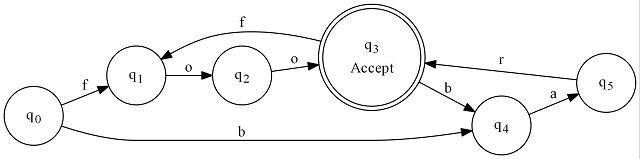
This graph looks totally different! If you follow it however, it will make sense. Also note that we have outgoing arrows from the double circled accepting state. The implication is such that we do not stop once we reach the accepting state until we can't continue - either because we can't find the next character match or because we ran out of input. We only care that it's accepting after we've matched as much as we can. This is called greedy matching. You can simulate lazy matching with more complicated expressions but there is no built in facility for that in non-backtracking regular expressions.
Building these graphs is a bit of a trick. The above graphs are known as DFAs but it's much easier to programmatically build graphs using NFAs. To implement NFAs, we add an additional type of line to the graph - dashed lines, we call epsilon transitions. Unlike input transitions, epsilon transitions do not consume any input or advance the input cursor. As soon as you are in a state, you are also in every state connected to it by a dashed line. Yes, we can be in more than one state at once now.
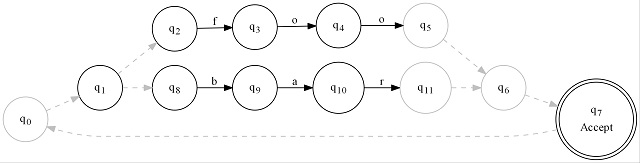
Two things that immediately stand out are the addition of the gray dashed lines and how much more intuitive the graph is. Remember that I said you automatically move into the states connected by epsilon transitions which means as soon as you are in q0, you are also in q1, q2, and q8. It can be said that the epsilon closure of q0 is { q0, q1, q2, q8 }. This is because of the dashed arrows leading out from each of the relevant states.
The above graph is much more expensive for a computer to navigate than the one that precedes it. The reason is that those epsilon transitions introduce the ability to be in multiple states at once. It is said to be non-deterministic.
The former graph is deterministic. It can only be in one state at a time, and that makes it much simpler for a computer to navigate it quickly.
An interesting property of these non-deterministic graphs is there's 1 equivalent deterministic graph. That is, there is one equivalent graph with no dashed lines/epsilon transitions in it. In other words, for any NFA there is 1 DFA that is equivalent. We'll be exploiting this property later.
Now that we know we can create these NFAs (with epsilon transitions) and later transform them to DFAs (without epsilon transitions), we'll be using NFA graphs for all of our state machine construction, only turning them into DFAs once we're finished.
We're going to use a variant of Thompson's construction algorithm to build our graphs. This works by defining a few elemental subgraphs and then composing those into larger graphs:
First, we have a literal - regex of ABC:
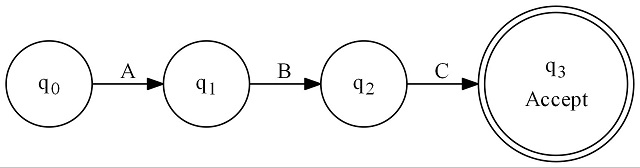
Next, we have a character set - regex of [ABC]:
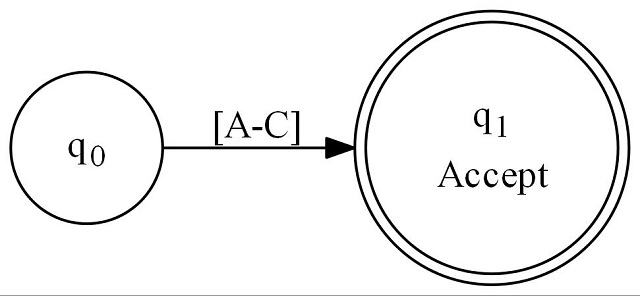
Next, we have concatenation - regex of ABC(DEF): (this is typically implicit)

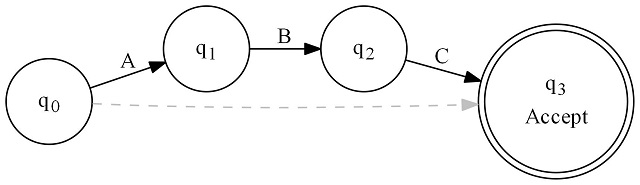
Now, we have or - regex of ABC|DEF:
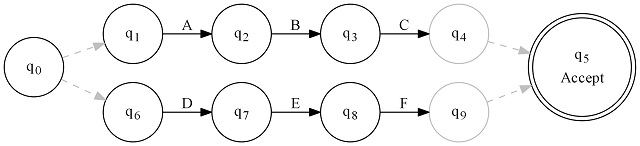
Next we have optional - regex of (ABC)?:
Finally, we have repeat - regex of (ABC)+:
Every other pattern you can do can be composed of these. We put these together a bit like legos to build graphs. The only issue is when we stick them together, we must make the former accepting states non accepting and then create a new accepting state for the final machine. Repeat this process, nested to compose graphs.
Note the grayed states with only a single outgoing dashed line. These are neutral states. They effectively do not do anything to change what the machine accepts, but they are introduced during the Thompson construction. This is fine, as it is a byproduct that will be eliminated once we transform the graph to a DFA.
Final states meanwhile, are simply states that have no outgoing transition. Generally, these states are also accepting.
These finite state machines are the heart of our regular expression engine.
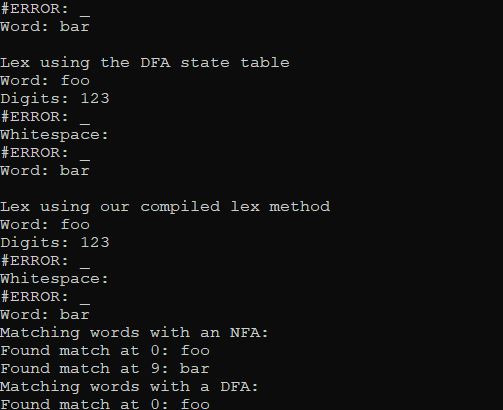
We'll be supporting tokenizing as a primary goal so I will attempt to explain it. Above, we have used "Accept" as our symbol - it appears below the state label (qX) in the double circled states. We can use other symbols, and we can have many different symbols per graph. Usually, such machines are called lexers. They are technically a hack of the math of a DFA, but they're a well worn hack used by every FSM based tokenizer under the sun. All it means is you can't represent it as a textual regex expression - it can only be created in code. Here's one that matches a series of digits, a series of letters (a "word"), or a string of whitespace, and it will report which of the 3 it is:
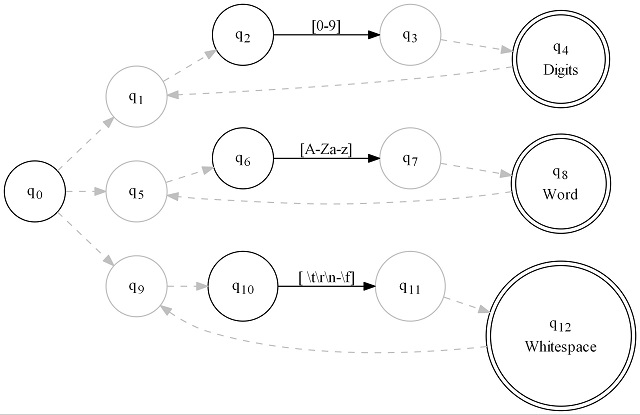
There is no true textual representation of a regular expression for this. It's a combination of other regular expressions. Each one has its own accept symbol associated with it. Furthermore, instead of running this machine once over a long string of text like we would with a traditional find-first match, we have to run this machine each time we "move" through the input. Basically, each time the machine is run, it advances the cursor over the input, so we just run the machine over and over again to move. Each iteration reports a symbol or an error.
So here, running it over the input string "foo123 bar" will report:
Word: foo
Digits: 123
Whitespace:
Word: barThis is why parsers typically rely on them. It basically breaks an input stream into a series of lexemes or tokens. Code that runs a machine like this is commonly referred to either as a tokenizer or a lexer. It's a specialty of our regular expression engine because that's the application where it's most useful under .NET.
Poweset construction once again, is how we turn an NFA into a DFA. We like this, because DFAs are much more efficient as we'll see later. What we need to do basically, is figure out all of the possible combinations of states we can be in. Each set of possible states will resolve roughly to one DFA state. The exception is when it's impossible such that two states transition to destination different states on the same input. At that point, we end up exploding the possibilities because we need to clone the path N-1 times where N is the number of conflicts. This is not easy to explain nor particularly easy to code. Hopefully, a figure will help:
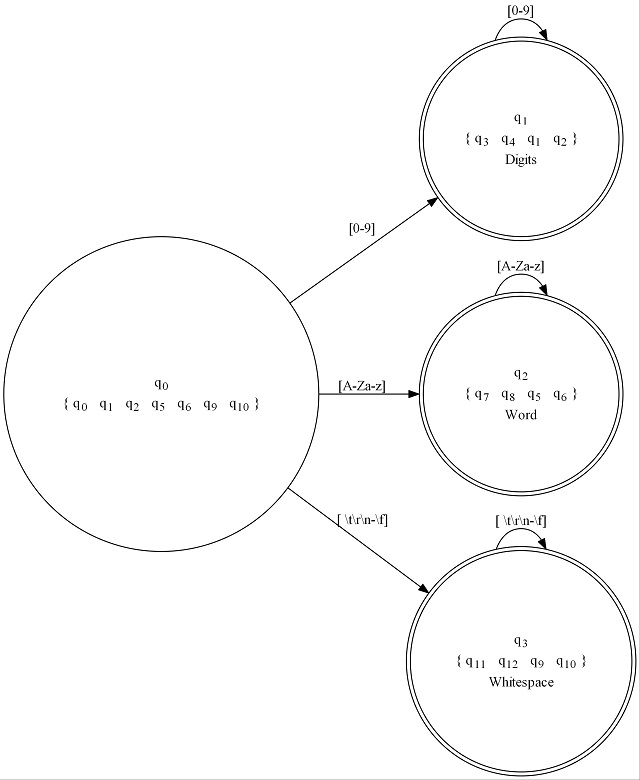
The graph indicates which of the source states the DFA state is composed of. You'll see that each state encompasses several of the other states. Sometimes however, a couple of states can yield a lot more states under the right - or rather wrong circumstances. I don't think I can explain the algorithm to you very clearly, but the code should help.
One thing you may have noticed is that the transition arrows sometimes have ranges above them. What it's actually doing is combining many arrows into one, and then assigning a range to that.
This is usually cosmetic, although the code is range aware and sometimes uses it for optimization, primarily during code generation or DFA state table traversal.
Speaking of DFA state tables, one nice thing about DFAs is it is relatively easy to reduce them to a state table, which allows for more efficient traversal. It's also easy to generate code from DFAs, but none of this is easy to do with NFAs.
A DFA state table looks like the following:
DFA State Table State Accept Inputs Destination q0 n/a [0-9] q1 q0 n/a [A-Za-z] q2 q0 n/a \s q3 q1 Digits [0-9] q1 q2 Word [A-Za-z] q2 q3 Whitespace \s q3
In our own classes, we use nested arrays to make this slightly more efficient, but the concept is the same.
Here's q2, as generated code:
q2:
if ((((context.Current >= 'A')
&& (context.Current <= 'Z'))
|| ((context.Current >= 'a')
&& (context.Current <= 'z'))))
{
// capture the current character under the cursor
context.CaptureCurrent();
// advance the input position by one
context.Advance();
// goto the next state (ourself)
goto q2;
}
return 1; // "Word" symbol idEither way, using a table, or using generated code, you can accomplish the same thing.
Anyway, hopefully this has made the concepts clear enough that we can start coding to them.
Coding this Mess
I've partitioned the CharFA
Let's start with the basic data structure of a single state in the state machine in CharFA.cs.
/// <summary>
/// Represents a single state in a character based finite state machine.
/// </summary>
/// <typeparam name="TAccept">The type of the accepting symbols</typeparam>
public partial class CharFA<TAccept>
{
// we use a specialized dictionary class both for performance and
// to preserve the order of the input transitions
/// <summary>
/// Indicates the input transitions.
/// These are the states that will be transitioned to on the specified input key.
/// </summary>
public IDictionary<char, CharFA<TAccept>> InputTransitions { get; }
= new _InputTransitionDictionary();
/// <summary>
/// Indicates the epsilon transitions.
/// These are the states that are transitioned to without consuming input.
/// </summary>
public IList<CharFA<TAccept>> EpsilonTransitions { get; }
= new List<CharFA<TAccept>>();
/// <summary>
/// Indicates whether or not this is an accepting state.
/// When an accepting state is landed on, this indicates a potential match.
/// </summary>
public bool IsAccepting { get; set; } = false;
/// <summary>
/// The symbol to associate with this accepting state.
/// Upon accepting a match, the specified symbol is returned which can identify it.
/// </summary>
public TAccept AcceptSymbol { get; set; } = default(TAccept);
/// <summary>
/// Indicates a user-defined value to associate with this state
/// </summary>
public object Tag { get; set; } = null;
/// <summary>
/// Constructs a new instance with the specified accepting value and accept symbol.
/// </summary>
/// <param name="isAccepting">Indicates whether or not the state is accepting</param>
/// <param name="acceptSymbol">Indicates the associated symbol to be used
/// when accepting.</param>
public CharFA(bool isAccepting,TAccept acceptSymbol=default(TAccept))
{
IsAccepting = isAccepting;
AcceptSymbol = acceptSymbol;
}
/// <summary>
/// Constructs a new non-accepting state
/// </summary>
public CharFA()
{
}
}There's not a whole lot here yet once you strip away the comments. It's mainly just some data fields and a couple of constructors:
First, we have InputTransitions. This is a dictionary of type IDictionary<char,CharFA
Next, we have EpsilonTransitions. This is a list of type IList<CharFA
IsAccepting indicates whether the state is accepting. Double circles in the graphs are accepting states.
AcceptSymbol indicates the accept symbol to associate with this state. This is used for tokenization. Each symbol is basically an id for the pattern it represents. Above, they were "Word", "Digits" and "Whitespace".
Finally, we have Tag. This property is for an arbitrary user defined value to associate with the state. This is typically used for debugging but it doesn't have to be. It has no effect on the machine.
Other than that, we simply have a convenience constructor and the default constructor.
Now, we need a way to do the basics of even finding the boundaries of the state machine. We need our closure functions! We can see that and other computation methods in CharFA.Computation.cs.
From now on, I will only highlight interesting portions of code as necessary, otherwise the article will be very long.
public IList<CharFA<TAccept>> FillClosure(IList<CharFA<TAccept>> result = null)
{
if (null == result)
result = new List<CharFA<TAccept>>();
else if (result.Contains(this))
return result;
result.Add(this);
// use a cast to get the optimized internal input mapping by FA state
foreach (var trns in InputTransitions as IDictionary<CharFA<TAccept>,ICollection<char>>)
trns.Key.FillClosure(result);
foreach (var fa in EpsilonTransitions)
fa.FillClosure(result);
return result;
}Basically, what we're doing here is recursively calling FillClosure() on any states we haven't seen before, adding them as we go. The check to see if we already have a state before recursing is important, otherwise a loop in the machine would cause a stack overflow in this function!
FillEpsilonClosure() works essentially the same way, but only traverses epsilon transitions.
Moving on, we have FillMove():
public static IList<CharFA<TAccept>> FillMove(IEnumerable<CharFA<TAccept>> states,
char input, IList<CharFA<TAccept>> result = null)
{
if (null == result) result = new List<CharFA<TAccept>>();
foreach (var fa in FillEpsilonClosure(states))
{
// examine each of the states reachable from this state on no input
CharFA<TAccept> ofa;
// see if this state has this input in its transitions
if (fa.InputTransitions.TryGetValue(input, out ofa))
foreach (var efa in ofa.FillEpsilonClosure())
if (!result.Contains(efa)) // if it does, add it if it's not already there
result.Add(efa);
}
return result;
}Remember when I said you can be in more than one state at once? Well, this function takes the set of states we're currently in and moves as indicated by the specified input character, yielding the set of states that it resulted in, after moving along all the necessary dashed gray lines and the solid black line, if one is applicable. Basically, it works simply by querying each input transition dictionary in turn for the input character after performing an epsilon closure. It then performs the epsilon closure of those result states in order to complete the operation. This is the heart of running a regular expression as this represents a single iteration of the regex character matching. This works on NFAs and DFAs but there's a more efficient way to move along DFAs since they can only be in one state. Consider MoveDfa():
public CharFA<TAccept> MoveDfa(char input)
{
CharFA<TAccept> fa;
if (InputTransitions.TryGetValue(input, out fa))
return fa;
return null;
}There are no loops or collections involved here. There is simply a dictionary lookup. This is much more efficient, but later, we'll make it more efficient still. Note that you can try this on an NFA but it won't work right. Unfortunately, while it's possible to check if a machine is a DFA or not, there's no way to do it efficiently enough for this method. Be sure to only use it with DFAs.
FillInputTransitionRangesGroupedByState() is a mouthful but it's descriptive. Each state is returned with a collection of inputs that lead to it. These inputs are returned as character ranges. This is primarily used for display and for code generation. The ranges are used to display the ranges above the input transitions and the code generator uses them for creating conditional statements.
I'd like to direct your attention to our optimized input transition dictionary in CharFA.InputTransitionDictionary.cs:
// a specialized input transition container dictionary.
// this isn't required for a working regex engine but
// can make some common operations significantly faster.
partial class CharFA<TAccept>
{
/// <summary>
/// This is a specialized transition container
/// that can return its transitions in 3 different ways:
/// 1. a dictionary where each transition state is keyed
/// by an individual input character (default)
/// 2. a dictionary where each collection of inputs is keyed
/// by the transition state (used mostly by optimizations)
/// 3. an indexable list of pairs where the key is the transition state
/// and the value is the collection of inputs
/// use casts to get at the appropriate interface for your operation.
/// </summary>
private class _InputTransitionDictionary :
IDictionary<char, CharFA<TAccept>>, // #1
IDictionary<CharFA<TAccept>, ICollection<char>>, // #2
IList<KeyValuePair<CharFA<TAccept>, ICollection<char>>> // #3
{
IDictionary<CharFA<TAccept>, ICollection<char>> _inner =
new ListDictionary<CharFA<TAccept>, ICollection<char>>();
...Internally, this class stores transitions as IDictionary<CharFA
Moving on, let's take a look at a monster of an equality comparer class in CharFA.SetComparer.cs:
partial class CharFA<TAccept>
{
// this class provides a series of comparers for various CharFA operations
// these are primarily used during duplicate checking and in the powerset
// construction
private sealed class _SetComparer :
IEqualityComparer<IList<CharFA<TAccept>>>,
IEqualityComparer<ICollection<CharFA<TAccept>>>,
IEqualityComparer<IDictionary<char, CharFA<TAccept>>>
{
...See my article on value equality semantics in C# for more about how equality comparers work. You can see this class implements three of them, each handling a different type of container. We use these in our scratch/working hashsets and dictionaries during powerset construction but also in other areas where we need to key a dictionary or hashtable by a collection of states or we need to compare input transitions (used by duplicate state detection code).
value equality semantics in C#
We can't do much without being able to build our state machines in the first place. Fortunately, we have a bunch of methods for doing so in CharFA.ThompsonConstruction.cs:
Each of the methods takes either an input string or one or more expressions, possible additional parameters, and finally, an optional accept symbol. This file provides the following constructions:
Literal(): This builds a literal given the input string.Set(): This builds a character set given the input string or collection of character ranges.Or(): This creates an alternation between two or more expressions. Basically, this will create a state machine that matches any of the specified expressions.Concat(): This creates a concatenation of two or more expressions in a series.Optional(): This creates a state machine that makes the passed in expression optional.Repeat(): This repeats an expression an optionally specified minimum and maximum number of times.CaseInsensitive(): This makes the specified expression case insensitive.
Each of these works by taking the passed in FSM/expression or string and creating a new FSM based on it. Typically, these methods connect the lines between the different states in order to fulfill the operation.
Consider Set():
public static CharFA<TAccept> Set(IEnumerable<char> set, TAccept accept = default(TAccept))
{
var result = new CharFA<TAccept>();
var final = new CharFA<TAccept>(true, accept);
foreach (var ch in set)
result.InputTransitions[ch]= final;
return result;
}What it does is create two new states, and then for each character in the set, it creates a transition from the first state to the final state, before returning the first state. This creates a graph as shown previously for character sets. Some of these can get quite complicated. Repeat() is an example of that simply because there are so many corner cases.
This is all well and good, but what if we need to look at the graph and examine what we just built? Sure we can dig through the dictionaries in the debugger, but what a pain! Instead, why not just be able to render the state machine to a jpeg or a png? Enter CharFA.GraphViz.cs:
This requires GraphViz, naturally, so make sure it is installed. This basically encompasses the whole grotty affair of using the GraphViz dot utility to render images from state machine graphs. Dot is pretty powerful, but also messy, a bit like Perl. The code to generate these dot specifications reflects this. Basically how it works is it takes the state machine and writes a dot spec to a stream which it pipes to the dot utility, and then pipes in the image that comes back. This requires GraphViz to be in your path, but it should be already as long as it's installed. There are a number of options you can get to via CharFA
var lit = CharFA<string>.Literal("ABC");
lit.RenderToFile("5251476/literal.jpg");This code takes care of all the terrible details. You can specify the output format via the file extension. For example, to render PNG files you'd use ".png" instead of ".jpg". I used this facility to render all the graphs for this article.
Finally, none of this is useful if we can't actually use the regular expressions to lex/tokenize or search text. This is what CharFA.Lexer.cs and CharFA.Matcher.cs are for:
partial class CharFA<TAccept>
{
/// <summary>
/// Creates a lexer out of the specified FSM "expressions"
/// </summary>
/// <param name="exprs">The expressions to compose the lexer with</param>
/// <returns>An FSM representing the lexer.</returns>
public static CharFA<TAccept> ToLexer(params CharFA<TAccept>[] exprs)
{
var result = new CharFA<TAccept>();
for (var i = 0; i < exprs.Length; i++)
result.EpsilonTransitions.Add(exprs[i]);
return result;
}
/// <summary>
/// Lexes the next input from the parse context.
/// </summary>
/// <param name="context">The <see cref="ParseContext"/> to use.</param>
/// <param name="errorSymbol">The symbol to report in the case of an error</param>
/// <returns>The next symbol matched - <paramref name="context"/>
/// contains the capture and line information</returns>
public TAccept Lex(ParseContext context,TAccept errorSymbol = default(TAccept))
{
TAccept acc;
// get the initial states
var states = FillEpsilonClosure();
// prepare the parse context
context.EnsureStarted();
while (true)
{
// if no more input
if (-1 == context.Current)
{
// if we accept, return that
if (TryGetAnyAcceptSymbol(states, out acc))
return acc;
// otherwise return error
return errorSymbol;
}
// move by current character
var newStates = FillMove(states, (char)context.Current);
// we couldn't match anything
if (0 == newStates.Count)
{
// if we accept, return that
if (TryGetAnyAcceptSymbol(states, out acc))
return acc;
// otherwise error
// store the current character
context.CaptureCurrent();
// advance the input
context.Advance();
return errorSymbol;
}
// store the current character
context.CaptureCurrent();
// advance the input
context.Advance();
// iterate to our next states
states = newStates;
}
}
/// <summary>
/// Lexes the next input from the parse context.
/// </summary>
/// <param name="context">The <see cref="ParseContext"/> to use.</param>
/// <param name="errorSymbol">The symbol to report in the case of an error</param>
/// <returns>The next symbol matched - <paramref name="context"/>
/// contains the capture and line information</returns>
/// <remarks>This method will not work properly on an NFA but will not error
/// in that case, so take care to only use this with a DFA</remarks>
public TAccept LexDfa(ParseContext context, TAccept errorSymbol = default(TAccept))
{
// track our current state
var state = this;
// prepare the parse context
context.EnsureStarted();
while (true)
{
// if no more input
if (-1 == context.Current)
{
// if we accept, return that
if(state.IsAccepting)
return state.AcceptSymbol;
// otherwise return error
return errorSymbol;
}
// move by current character
var newState = state.MoveDfa((char)context.Current);
// we couldn't match anything
if (null == newState)
{
// if we accept, return that
if (state.IsAccepting)
return state.AcceptSymbol;
// otherwise error
// store the current character
context.CaptureCurrent();
// advance the input
context.Advance();
return errorSymbol;
}
// store the current character
context.CaptureCurrent();
// advance the input
context.Advance();
// iterate to our next states
state = newState;
}
}
public static int LexDfa(CharDfaEntry[] dfaTable,
ParseContext context, int errorSymbol = -1)
{
// track our current state
var state = 0;
// prepare the parse context
context.EnsureStarted();
while (true)
{
// if no more input
if (-1 == context.Current)
{
var sid = dfaTable[state].AcceptSymbolId;
// if we accept, return that
if (-1 != sid)
return sid;
// otherwise return error
return errorSymbol;
}
// move by current character
var newState = MoveDfa(dfaTable, state, (char)context.Current);
// we couldn't match anything
if (-1 == newState)
{
// if we accept, return that
if (-1 != dfaTable[state].AcceptSymbolId)
return dfaTable[state].AcceptSymbolId;
// otherwise error
// store the current character
context.CaptureCurrent();
// advance the input
context.Advance();
return errorSymbol;
}
// store the current character
context.CaptureCurrent();
// advance the input
context.Advance();
// iterate to our next states
state = newState;
}
}
}You can see we've introduced a new class, called ParseContext. This class handles cursor position tracking and capturing during a lex or a match. It can also be used to implement hand rolled parsers, which was what it was designed for. See my Code Project article on it for more information. A ParseContext can be created over any instance of IEnumerable
Code Project article 1.0 version
The matching functionality is very similar so we won't cover the implementation here.
The three methods here all do the same thing using different mechanisms. They are listed in order of performance, worst to best. The better ones take upfront prep - converting to a DFA or a DFA state table but they perform better. They are fairly simple to use. Each one operates almost the same way, but lexing a DFA table is slightly more complicated because the symbols are mapped to ints and you use a symbol table to resolve them.
// create a parse context over our test string
var pc = ParseContext.Create(test);
// while not end of input
while (-1 != pc.Current)
{
// clear the capture so that we don't keep appending the token data
pc.ClearCapture();
// lex the next token, using #ERROR as our error symbol
var acc = lexer.Lex(pc, "#ERROR");
// write the result
Console.WriteLine("{0}: {1}",acc, pc.GetCapture());
}Using matching to search through a string looks like this:
CharFAMatch match;
var pc = ParseContext.Create(test);
while (null!=(match=word.Match(pc)))
Console.WriteLine("Found match at {0}: {1}", match.Position, match.Value);We just keep calling Match() or MatchDfa() until it returns null.
What about parsing actual textual regular expression? What if we want to create a CharFA
RegexExpression.Parse() is how we get a regular expression DOM from its textual representation. It uses recursive descent parsing to build the DOM.
The following DOM expressions are available:
RegexExpression: The abstract base of all other expressions.RegexUnaryExpression: An abstract base for an expression that has one target expression.RegexBinaryExpression: An abstract base for an expression that has a left and a right target expression.RegexCharsetExpression: Represents[]expressions. Supports many POSIX character classes.RegexConcatExpression: Represents regex concatenation, such asABC.RegexLiteralExpression: Represents a single literal character such asA.RegexOptionalExpression: Represents the?modifier.RegexOrExpression: Represents|alternation.RegexRepeatExpression: Represents*,+and{,}modifiers.
Here's a brief example of how to use the DOM:
var test = "(ABC|DEF)*";
var dom = RegexExpression.Parse(test);
Console.WriteLine(dom.ToString());
var rep = dom as RegexRepeatExpression;
rep.MinOccurs = 1;
Console.WriteLine(dom.ToString());
var fa = dom.ToFA("Accept");Which outputs:
(ABC|DEF)*
(ABC|DEF)+And creates a state machine graph of:

Now, in order to transform something like the above to a DFA, we need to perform powerset construction.
The code for this is in CharFA.PowersetConstruction.cs:
partial class CharFA<TAccept>
{
/// <summary>
/// Transforms an NFA to a DFA
/// </summary>
/// <param name="progress">The optional progress object used to report
/// the progress of the operation</param>
/// <returns>A new finite state machine equivalent to this state machine
/// but with no epsilon transitions</returns>
public CharFA<TAccept> ToDfa(IProgress<CharFAProgress> progress = null)
{
// The DFA states are keyed by the set of NFA states they represent.
var dfaMap = new Dictionary<List<CharFA<TAccept>>,
CharFA<TAccept>>(_SetComparer.Default);
var unmarked = new HashSet<CharFA<TAccept>>();
// compute the epsilon closure of the initial state in the NFA
var states = new List<CharFA<TAccept>>();
FillEpsilonClosure(states);
// create a new state to represent the current set of states. If one
// of those states is accepting, set this whole state to be accepting.
CharFA<TAccept> dfa = new CharFA<TAccept>();
var al = new List<TAccept>();
// find the accepting symbols for the current states
foreach (var fa in states)
if (fa.IsAccepting)
if (!al.Contains(fa.AcceptSymbol))
al.Add(fa.AcceptSymbol);
// here we assign the appropriate accepting symbol
int ac = al.Count;
if (1 == ac)
dfa.AcceptSymbol = al[0];
else if (1 < ac)
dfa.AcceptSymbol = al[0]; // could throw, just choose the first one
dfa.IsAccepting = 0 < ac;
CharFA<TAccept> result = dfa; // store the initial state for later,
// so we can return it.
// add it to the dfa map
dfaMap.Add(states, dfa);
dfa.Tag = new List<CharFA<TAccept>>(states);
// add it to the unmarked states, signalling that we still have work to do.
unmarked.Add(dfa);
bool done = false;
var j = 0;
while (!done)
{
// report our progress
if (null != progress)
progress.Report(new CharFAProgress(CharFAStatus.DfaTransform, j));
done = true;
// a new hashset used to hold our current key states
var mapKeys = new HashSet<List<CharFA<TAccept>>>(dfaMap.Keys, _SetComparer.Default);
foreach (var mapKey in mapKeys)
{
dfa = dfaMap[mapKey];
if (unmarked.Contains(dfa))
{
// when we get here, mapKey represents the epsilon closure of our
// current dfa state, which is indicated by kvp.Value
// build the transition list for the new state by combining the transitions
// from each of the old states
// retrieve every possible input for these states
var inputs = new HashSet<char>();
foreach (var state in mapKey)
{
var dtrns = state.InputTransitions as
IDictionary<CharFA<TAccept>, ICollection<char>>;
foreach (var trns in dtrns)
foreach (var inp in trns.Value)
inputs.Add(inp);
}
// for each input, create a new transition
foreach (var input in inputs)
{
var acc = new List<TAccept>();
var ns = new List<CharFA<TAccept>>();
foreach (var state in mapKey)
{
CharFA<TAccept> dst = null;
if (state.InputTransitions.TryGetValue(input, out dst))
{
foreach (var d in dst.FillEpsilonClosure())
{
// add the accepting symbols
if (d.IsAccepting)
if (!acc.Contains(d.AcceptSymbol))
acc.Add(d.AcceptSymbol);
if (!ns.Contains(d))
ns.Add(d);
}
}
}
CharFA<TAccept> ndfa;
if (!dfaMap.TryGetValue(ns, out ndfa))
{
ac = acc.Count;
ndfa = new CharFA<TAccept>(0 < ac);
// assign the appropriate accepting symbol
if (1 == ac)
ndfa.AcceptSymbol = acc[0];
else if (1 < ac)
ndfa.AcceptSymbol = acc[0]; // could throw, instead just set it
// to the first state's accept
dfaMap.Add(ns, ndfa);
// work on this new state
unmarked.Add(ndfa);
ndfa.Tag = new List<CharFA<TAccept>>(ns);
done = false;
}
dfa.InputTransitions.Add(input, ndfa);
}
// we're done with this state
unmarked.Remove(dfa);
}
}
++j;
}
return result;
}
}Ooooh, that's ugly. The sordid truth is I spent ages getting it working a long time ago in a previous incarnation of my regex engine. It has been evolved over time. I only vaguely understand the math involved, so I haven't tried to recode it from scratch even though it could probably use it. The good news is, it works. Using ToDfa() is straightforward, but the progress parameter deserves some explanation. It follows Microsoft's IProgress
We have a related mechanism to generate a DFA state table in CharFA.DfaStateTable.cs. It contains ToDfaStateTable() which takes an optional (but recommended) symbol table that is simply an array of TAccept. It maps them to ids such that the id is the index of the TAccept symbol in the array. Since the table based DFA only uses integers, this table is used to map them back to symbols. The created table can be passed to the static XXXXDfa() methods.
Our engine is now feature complete, sans code generation, so that is what we'll cover next. Let's visit CharFA.CodeGeneration.cs:
This code supports two major styles of code generation; it can simply serialize the dfa table and symbol tables to code (table driven) or it can actually generate compilable state machine code using gotos. Generally, it's recommended to use the table driven approach as they are roughly the same speed unless the state machine is large, in which case the table driven form overtakes the compiled form. The compiled form is mainly included for curiosity and illustrative purposes. Keep in mind either way that the release builds will be much faster.
Serialization of the table driven arrays are performed via GenerateSymbolTableInitializer() and GenerateDfaStateTableInitializer(). Each returns a Code DOM expression that can be used to initialize a field or a variable.
Typically, what you'll do is use the Code DOM to build a class, then for each generated regular expression or lexer, you will serialize one or two read-only static member fields on that class: the symbol table, if using a lexer, and the DFA state table in either case. You can then use these fields at runtime like you would a normal runtime DFA state table, passing them to LexDfa(), or MatchDfa() as appropriate. When using the lexer, you will use the symbol table to resolve the accept symbols as shown below:
pc = ParseContext.Create(test);
while (-1 != pc.Current)
{
pc.ClearCapture();
var acc = CharFA<string>.LexDfa(GeneratedLexDfaTable, pc, 3);
// when we write this, we map our symbol id back to the
// symbol using our symbol table.
Console.WriteLine("{0}: {1}", GeneratedLexSymbols[acc], pc.GetCapture());
}This is the easiest code generation option, and is best for general purpose use.
The other way to generate code is through the GenerateMatchMethod() and GenerateLexMethod() methods, which generate compile-ready code using gotos. These don't require a DFA table, but you will need to use a symbol table in tandem with the lex method, so use the aforementioned method to generate that. You'll have to name the methods and set the access modifiers appropriately before you use them.
Typically, as before you'll use the Code DOM to build a class, and then for each generated regular expression or lexer, you will use the above to create a static method (and an associated symbol table field for the lexers) on the class. Often, you will generate both lex and match methods plus one symbol table field for each expression. That's three members in total to be clear, in order to have the full regex capabilities. If you don't need lexing, you can leave it out, or similar with matching. To be clear, if all you need is matching you'll just have the one static method per expression. If all you need is lexing, you'll have one static method and one static read-only field for each. If you need both lexing and matching, you'll have two methods and one field per for a total of three members per expression.
Be conservative in your use of this as the compiled methods can become large pretty quickly. The arrays wind up large in the source too, but it's mostly whitespace. Also keep in mind, there is a slight overhead on startup with the table driven versions because of the static field initializers, so if you have a large number of these, your app may stall a little on startup. This is still much quicker than building the state machine at runtime, no matter how you do it.
Let's explore the compiled version by revisiting our DFA lexer graph (this time without the extra clutter):
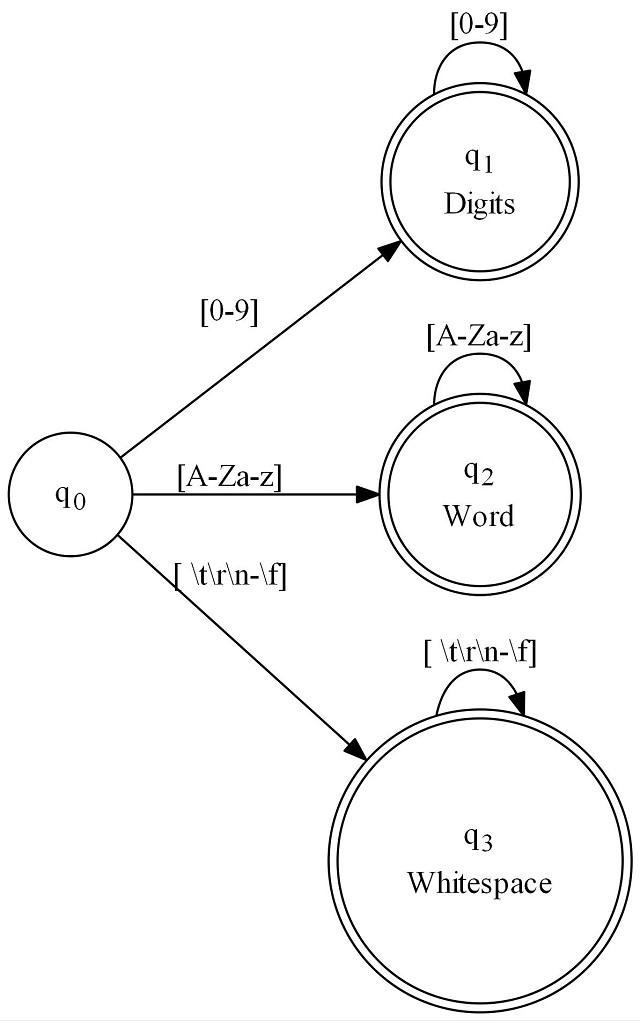
Keep this figure in mind. Now let's look at the default generated code for it:
internal static int Lex(RE.ParseContext context)
{
context.EnsureStarted();
// q0
if (((context.Current >= '0')
&& (context.Current <= '9')))
{
context.CaptureCurrent();
context.Advance();
goto q1;
}
if ((((context.Current >= 'A')
&& (context.Current <= 'Z'))
|| ((context.Current >= 'a')
&& (context.Current <= 'z'))))
{
context.CaptureCurrent();
context.Advance();
goto q2;
}
if (((((context.Current == '\t')
|| ((context.Current >= '\n')
&& (context.Current <= '
')))
|| (context.Current == '\r'))
|| (context.Current == ' ')))
{
context.CaptureCurrent();
context.Advance();
goto q3;
}
goto error;
q1:
if (((context.Current >= '0')
&& (context.Current <= '9')))
{
context.CaptureCurrent();
context.Advance();
goto q1;
}
return 0;
q2:
if ((((context.Current >= 'A')
&& (context.Current <= 'Z'))
|| ((context.Current >= 'a')
&& (context.Current <= 'z'))))
{
context.CaptureCurrent();
context.Advance();
goto q2;
}
return 1;
q3:
if (((((context.Current == '\t')
|| ((context.Current >= '\n')
&& (context.Current <= '
')))
|| (context.Current == '\r'))
|| (context.Current == ' ')))
{
context.CaptureCurrent();
context.Advance();
goto q3;
}
return 2;
error:
context.CaptureCurrent();
context.Advance();
return 3;
}If you compare the previous graph figure to the code above, you can see how they line up: Each state is represented by a label in the graph - except the first state, which is indicated by a comment since it's never jumped to. Each transition range meanwhile, is indicated by the relevant conditions in the if statements. There is one if for each possible destination state. CaptureCurrent() just stores the character at the cursor, while Advance() simply moves the cursor forward by one character. Each of the returned accept symbol ids is hard coded. The error condition knows to return 3 because we passed it into the generation method. Other than that, the code is very straightforward.
Usually, you'll want to change the name of the method and perhaps the access modifiers before you use it. The above are just the default.
The table generation methods aren't as interesting since they simply produce array initializer expressions. We won't cover the generated code here but the included demo project does. The two table generation methods use _Serialize() which recursively creates Code DOM expressions to instantiate the values in instances or arrays. In order to get CharDfaEntry and CharDfaTransitionEntry to serialize we use Microsoft's component model type descriptor framework, and have two custom type converters in CharDfaEntry.cs which tell our code how to serialize the respective types. It uses InstanceDescriptor which is a bit arcane, but see this article for details on how it works.
Generally, you'll create a class with the Code DOM, and then add methods or fields you generate to it:
The process for generating both compiled and table driven lex code is shown below:
// create the symbol table (include the error symbol at index/id 3)
var symbolTable = new string[] { "Digits", "Word", "Whitespace", "#ERROR" };
// create the DFA table we'll use to generate code
var dfaTable = lexer.ToDfaStateTable(symbolTable);
// create our new class - in production we'd change the name
// to something more appropriate
var compClass = new CodeTypeDeclaration("RegexGenerated");
compClass.TypeAttributes = System.Reflection.TypeAttributes.Class;
compClass.Attributes = MemberAttributes.Final | MemberAttributes.Static;
// add the symbol table field - in production we'll change the name
var symtblField = new CodeMemberField(typeof(string[]), "LexSymbols");
symtblField.Attributes = MemberAttributes.Static | MemberAttributes.Public;
// generate the symbol table init code
symtblField.InitExpression = CharFA<string>.GenerateSymbolTableInitializer(symbolTable);
compClass.Members.Add(symtblField);
// Generate and add the compiled lex method code
compClass.Members.Add(CharFA<string>.GenerateLexMethod(dfaTable, 3));
// in production we'd change the name of the returned method
// above
// add the DFA table field - in production we'd change the name
var dfatblField = new CodeMemberField(typeof(CharDfaEntry[]), "LexDfaTable");
dfatblField.Attributes = MemberAttributes.Static | MemberAttributes.Public;
// generate the DFA state table init code
dfatblField.InitExpression = CharFA<string>.GenerateDfaStateTableInitializer(dfaTable);
compClass.Members.Add(dfatblField);
// create the C# provider and generate the code
// we'll usually want to put this in a namespace
// but we haven't here
var prov = CodeDomProvider.CreateProvider("cs");
prov.GenerateCodeFromType(compClass, Console.Out, new CodeGeneratorOptions());You'd want to repeat this on this class for every expression. I recommend using a partial class for each expression as the source already gets long. The mechanism is similar, but slightly easier for generating match methods, because those do not need a symbol table field.
Using the compiled Lex() method is exactly like using the DFA state table version of LexDfa(), except easier. You do not have to pass a DFA state table or the error symbol as those are already "baked in" to the method and constant. You still have to map symbol ids back to their symbols using the symbol table. This is for performance reasons when it comes to parsers, which tend to deal with symbols as int ids internally.
Generating a compiled match method using GenerateMatchMethod() is essentially the same, minus the error symbol id, which it doesn't need. Using the compiled match method is the same as using the static MatchDfa() method, except you don't pass the DFA state table. See the code well above for how to do matching. You also won't need to generate a symbol table.
We're now feature complete. The rest of the code files are either support or gold plating. This should provide you a solid foundation for crafting your own regular expression engine or modifying this one. Hopefully, you have enjoyed the journey.
History
- 20th November, 2019 - Initial submission