How to Make an LL(1) Parser: Lesson 3
Updated on 2019-07-14
Creating a simple parser in 3 easy lessons
Introduction
We are now at long last, going to build a parser with what we created in lesson 1 and lesson 2.
Background
All we need to do is drive a tokenizer and a parse table in conjunction with a stack and we'll have what's known as a pushdown-automata (PDA) which we can use to parse.
We'll be using the stack to keep track of our tree, and we'll be using the input tokenizer to get tokens with which to parse, while our parse table is used for matching the token symbols to rules.
When we encounter a rule, we traverse it, pushing its derivation onto the stack and thus adding it to the parse tree.
We also have to be careful about error conditions. We do a form of simple error recovery called "panic-mode error recovery" in an attempt to keep parsing in the event of an error, while still reporting the error.
Runthrough
We can once again head back to Andrew Begel's paper if we want another alternative explanation of the process.
Here is our parse table, for reference.
- * ( ) int #EOS E E-> T E' E-> T E' E' E' -> + T E' E' -> E' -> T T-> F T' T-> F T' T' T'-> T'-> * F T' T'-> T'-> F F-> ( E ) F-> int
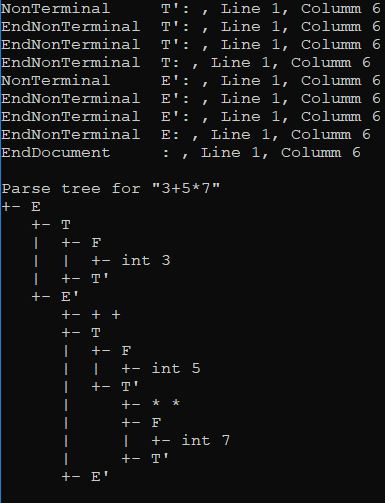
We are going to consider the input string "3+5*7".
When we start, our stack must be empty. The very first thing we do is push the "start symbol" onto the stack. For our grammar, that's E, since it's the first non-terminal in the grammar. We also now need to read the next token from the tokenizer and store it, even though we won't be using it just yet.
Our stack is { E } so far. Our tokenizer is positioned over 3, which is an int.
Since we have an E on the stack, and our input symbol is int, we pick the transition E -> T E' from the table. This means, we must pop E off the stack and them push its derivation T E'. on to the stack (which we do in reverse order)
Note that one additional thing our parser does that others may not is we push special markers onto the stack to indicate the end of a non-terminal. We won't consider those here since they aren't part of the actual parse tree - they just help us figure out where non-terminals begin and end.
So now anyway, our stack is { T, E' } and we're still on an int in the input. Looking at the table for row T and input int, we find T -> F T' so once again, we pop from the stack, removing T and then push its derivation onto the stack.
That leaves our stack at { F, T', E' } and we're still on an int in the input. Looking at the table for row F and input int, we find F -> int so once again, we pop from the stack, removing F and then push its derivation onto the stack, which is now { int, T', E' }
At last, since the top of our stack is int and so is our input, we pop the stack, and advance the tokenizer.
Now our stack is { T', E' } and this time, our input is on + which gives us rule T'-> so we simply pop the stack.
It goes on like this until we're done and an #EOS is entered.
Coding this Mess
The main class here to consider is Parser and we need one so let's create it for our input.
// create a parser using our
// parse table and lexer, and
// input text
var text = "3+5*7";
var parser = new Parser(
cfg.ToParseTable(),
new Tokenizer(lexer, text),
"E");The parser itself works similarly to an XmlReader so if you're familiar with the Read/NodeType pattern involved in that, this is going to be a breeze for you to learn to use.
It also contains a ParseSubtree method you can use to reader the current subtree into a parse tree if you'd rather deal with that.
The heart of the parser is the Read method:
public bool Read()
{
var n = NodeType;
// early exit if we're in the middle of handling an error
if (ParserNodeType.Error == n && "#EOS" == _tokEnum.Current.Symbol)
{
_errorToken.Symbol = null;
_stack.Clear();
return true;
}
// initialize the stack on the first read call and advance the input
if (ParserNodeType.Initial == n)
{
_stack.Push(_startSymbol);
_tokEnum.MoveNext();
return true;
}
_errorToken.Symbol = null; // clear the error status
if(0<_stack.Count) // there's still more to parse
{
var sid = _stack.Peek(); // current symbol
if(sid.StartsWith("#END ")) // end non-terminal marker
{
_stack.Pop();
return true;
}
// does the stack symbol match the current input symbol?
if(sid==_tokEnum.Current.Symbol) // terminal
{
// lex the next token
_tokEnum.MoveNext();
_stack.Pop();
return true;
}
// non-terminal
// use our parse table to find the rule.
IDictionary<string, CfgRule> d;
if(_parseTable.TryGetValue(sid, out d))
{
CfgRule rule;
if(d.TryGetValue(_tokEnum.Current.Symbol, out rule))
{
_stack.Pop();
// store the end non-terminal marker for later
_stack.Push(string.Concat("#END ", sid));
// push the rule's derivation onto the stack in reverse order
var ic = rule.Right.Count;
for (var i = ic - 1; 0 <= i;--i)
{
sid = rule.Right[i];
_stack.Push(sid);
}
return true;
}
_Panic(); // error
return true;
}
_Panic(); // error
return true;
}
// last symbol must be the end of the input stream or there's a problem
if ("#EOS" != _tokEnum.Current.Symbol)
{
_Panic(); // error
return true;
}
return false;
}More on using the code is shown in the Lesson 3/Program.cs file.
And that's about it!
History
- 14th July, 2019 - Initial submission