Metaprogramming in C++: A Gentle Introduction
Updated on 2021-03-23
Make your code more efficient by hacking your compiler to improve its optimization capabilities
Introduction
I was working on a graphics library recently that provides a rich array of compile-time information about every aspect of it. You can do things like get information about each color channel of a pixel, like its name, or how many bits it takes to represent it.
Everything possible is computed at compile time, since this library is primarily for tiny devices, and they can't afford the runtime overhead that would allow for much of the functionality provided by this library at compile time.
One especially challenging bit was finding a particular channel for a pixel by name - at compile time of course. I'm embarrassed to say it took me the better part of a day, so I'm presenting this article in the hopes that you don't run into the same problem.
Note that everything here will compile with the C++11 standard. C++11 doesn't have a lot of the sugar and features of later standards when it comes to metaprogramming, which actually makes it a good candidate for demonstrating the basic techniques, without new language features obscuring the mechanics.
Note: Template instantiations create long lines of code. It's just how things are. I've done my best to try to reformat the code so it's presentable on this site, but in terms of code formatting, I had to deprioritize that and focus on getting the code to fit within the confines of the web page width. My point is the code formatting leaves something to be desired because it was written so that it didn't wrap all over the place on the website rather than written for utmost readability in terms of code structure.
A Metaprogramming Crash Course
I'd like to start by reiterating something that Bjarne Stroustrup gets on about when it comes to C++ - if anything, it's about templates, not about objects as a primary paradigm.
To code in C++ is to use templates. If you aren't using them, you're avoiding a primary language feature. In essence, you're not really using C++ unless you're using templates. If you're using C++ for its OO capabilities, consider another language, because while C++ can do OOP, it is not the most effective language when using OOP as a primary paradigm.
Now:
// construct a 16-bit RGB color pixel
// in big endian format. with 5,6,
// and 5 bits for R, G, and B,
// respectively:
using rgb565be = typed_pixel<
color_model::rgb,
endian_mode::big_endian,
channel_traits<channel_name::R,5>, // red
channel_traits<channel_name::G,6>, // green
channel_traits<channel_name::B,5> // blue
>;
// retrieve the red color channel (named "R")
using the_channel =
typename rgb565be::channel_type_by_name<
channel_name::R>;This deceptively simple bit of code was very challenging for me to implement, but then I'm still building up my metaprogramming skills. Anyway, all it does is construct a 3 channel RGB pixel with a particular binary format, and then hunt through the pixel's type definition by name for the R channel. It does nothing at run-time - this is all using compile-time computations involving metaprogramming. As with the above, this technique is useful for retrieving named arguments out of a variadic template by their name.
If you've never used variadic templates, and you don't know what a parameter pack is, you may want to follow these links for more information on them and brush up because we're going to make use of them here. In fact, they're central to this article, but I explain them fairly extensively below.
variadic templates parameter pack
Before we even get to those however, we need to cover some basics. Many of these basics are already provided for in the STL but understanding how they work is important so we'll be implementing similar templates in this code.
Approaching O(log N)•0
Here •0 is the operating idea. The most efficient code is the code that never runs. The reason for metaprogramming is to make your applications more efficient by offloading work onto the compiler wherever possible. This takes advantage of the advanced nature of a modern C++ compiler, and its heavy optimization capabilities, and extends the capabilities of those well beyond what they were originally intended for.
This "extended use" of the C++ compiler's optimization features is pretty much hacking. That's the bad news. The code is counterintuitive and winds up being voodoo to the untrained eye, and can be difficult to follow even for seasoned developers, though its power and flexibility can make up for it when you need it.
Despite the downsides of metaprogramming, as C++ evolves, metaprogramming techniques are being incorporated as "first class" elements of the language, making them clearer, more integrated and thus easier to follow and maintain. Due to that, it's a good idea to get up to speed with C++ metaprogramming techniques since C++11.
There is No Type
Types don't really exist. That's right. They aren't "real." What I mean by this is that your running, binary code has absolutely no concept of types. Types are simply an organizational tool and a facility that tells you how to interpret the data it points to. A type, at best is an abstract facade. For example, a struct with fields in it simply lets the compiler know what offsets into memory each field of data exists at. When the program is compiled, those offsets are "baked in" to the code and the type definition itself is discarded. You're not accessing customer.name - you're accessing a particular offset in the stack (or a location on the heap). This is why you need things like RTTI to get type information at run-time, and symbols to get type information in the debugger. Think of types like concrete molds. They give shape to your data, but once the data is set, the mold/type is no longer needed.
The reason this is important is that the techniques herein can sometimes create hundreds or thousands of types, often recursively. By itself, this has no impact on your running code, but it does have an impact on how long it takes to compile your code because the compiler has to keep track of all of that.
Faciō Ergō Sum
"I create, therefore I am" - your compiler. To create is to compute. If we want to solve an algorithm at compile-time, it often involves creating types as part of the process. I'll explain:
There are two primary ways to convince the compiler to do non-trivial computations for you. You can use constexpr to indicate to the compiler that a function can be executed by the compiler and its result used at compile time. This can be useful for example, for computing prime numbers and letting the compiler deal with providing the values rather than computing your static lookup table when the program starts. The compile-time mechanism has zero overhead so it's infinitely more efficient in terms of CPU time. You'll still need the actual table for your run-time code but this way, you don't have to compute it at run-time.
The other way to do it is template instantiation and folding. Folding is nothing fancy. Pretty much every language does it. It's simply the process of solving equations where all values are known at compile time, such as:
static const int a = 2;
static const int b = 3;
// c is "folded" to 6:
static const int c = a * b;The template instantiation primarily involves templates (often that fold values) while recursively instantiating further templates until a terminating specialization is reached. Here's a simple example that computes pow() for ints at compile time:
// analog to pow() at compile time
template<int X,int Y> struct power {
constexpr static const long long value =
X * power<X,Y-1>::value;
};
// terminating specialization
template<int X> struct power<X,0> {
constexpr static const long long value = 1;
};Note how we have the base template and a specialization. You'll virtually always need a specialization for the terminating condition of any recursive template instantiation. Here, our terminating condition is where Y = 0, as indicated by the second template declaration.
The key here however, is in our first template declaration. Look how we're folding the result of a multiplication with the current X argument with the result from a recursive instantiation of our template, decrementing Y by one. When Y reaches zero, it will trigger our specialization, which simply returns 1. There's the magic. All of this winds up being folded into a single final value by the compiler because every single value is constant and known at compile time.
For power<2,8>, we end up folding 222222221. Our template instantiations look like this:
struct power<2,8> {
constexpr static const long long value =
2 * power<2,7>::value;
};
struct power<2,7> {
constexpr static const long long value =
2 * power<2,6>::value;
};
...
struct power<2,1> {
constexpr static const long long value =
2 * power<2,0>::value;
};
struct power<2,0> {
constexpr static const long long value =
1;
};That's pretty straightforward once you get the hang of it. This technique of recursive instantiation to do iteration is really important because so much of metaprogramming relies on it that you can't get very far without it.
Just so you know, I'm not yanking your chain about this being done at compile time, take a look at the output from Compiler Explorer with -fwhole-program -Os -std=c++11:
.LC0:
.string "power<2,8> = %lli\r\n"
main:
push rax
mov esi, 256
mov edi, OFFSET FLAT:.LC0
xor eax, eax
call printf
xor eax, eax
pop rdx
retThat's the entire application in assembly using the C++ code presented just above it. Notice the bolded line. The compiler simply replaced power<2,8>::value with 256! Most of the code is simply calling printf() and then returning from main().
Computing powers might not be the most useful thing in the world but what about computing trig functions? With a little work, you could make a negative power "function" to complement the above, and then another function to run a power series expansion to compute say, tangents up to a particular resolution. That's a little extreme, but I'm just illustrating what's possible. As I said before, you don't need to waste cycles at startup computing static lookup tables anymore.
power series expansion tangents
You might have noticed the use of constexpr above. I use it a lot when metaprogramming - certainly more than I really need to, but with good reason. While constexpr simply indicates that something can be resolvable at compile time, the compiler usually doesn't need it in order to know that. However, if you use constexpr, it not only clarifies intent - this code is for the compiler, and might not be used at run time at all - it also enforces the restrictions the compiler places on code it is willing to execute. For example, if you use it on a function definition, you can't do things like call printf() because what would that even do at compile time? It wouldn't make any sense. You also can't do things like infinite loops, for obvious reasons. Using constexpr, the compiler errors if I color outside the lines, rather than simply putting the function into the run-time code and then calling that during the program's execution. Note that I said it can be called at compile time. Such fields and functions can also be referenced by running code, in which case, the code for those fields and functions will be inserted by the compiler for use by the run-time code, regardless of the compiler running it at compile time.
The Myth of Code Bloat
C++ templates are often criticized for introducing code bloat. I think one reason is that the STL was designed to be more general purpose than it was efficient in terms of priorities. Another reason I think, is that it is easy to cause the compiler to duplicate code, especially with poorly designed templates. Finally, C++ compilers used to be not so great at removing all of the "dead code" templates introduced, but that's not even remotely the case with modern compilers.
The truth, as it so often is, is more complicated.
It's true that it's easy to write templates poorly, and to potentially cause the compiler to create two or more copies of nearly identical code. The answer to this is to always look at the output of your template instantiations in something like Compiler Explorer linked to above. I tend to prototype my templates in a separate application all in one main.cpp file to ease pasting into Compiler Explorer so I can isolate them and see what they're producing when instantiated.
All that having been said, well written templates can dramatically shrink your code while increasing performance and even reducing your application's memory footprint. The reasons are as already alluded to - the most efficient code is the code that is never run, or better yet, never compiled into your binary. This is what I mean when I say "O(log n)•0". Template and constexpr function metaprogramming can eliminate the need to provide the memory and CPU power to do computations at run time. You can generate specific code to meet your use case, and eliminate the code that handles the general cases using effective metaprogramming techniques. That way, your code can maintain its flexibility through templating, while increasing the run-time efficiency of your code. Metaprogramming effectively allows you to "guide" the compiler into complicated optimizations it wouldn't otherwise know to make. Eliminating the startup computation time for generating static lookup tables as we did above was one simple example of this in the wild.
Move Over Typedef
In case you're not familiar with the new use of the using keyword, it now supplants typedef as a more powerful alternative for aliasing types. Unlike typedef, using can be used to alias templates, not just template instantiations:
using int_t = int; // equivalent to typedef int int_t;
// the following is a template alias
template<typename X,typename Y> using pair_vector
= std::vector<std::pair<X,Y>>;Going Meta with Variadic Templates
Variadic templates accept any numer of template arguments. They are a powerful feature that adds significant flexibility to your code. Unfortunately, they can be difficult to use.
You can declare a variadic template using syntax like the following:
template<typename... Args> struct variadic_example {};Args is called a "parameter pack", and it can be "expanded" basically into a series of comma separated values representing each of the arguments that was given to it. It's weirdly lexical, in that it really does expand into comma separated values, rather than something more, I guess "formal", like any kind of real list or array. It reminds me of environment variable expansion, if you catch my meaning, and I find it helps to think of it like that.
The Parameter Pack
A "parameter pack" is the variable list of arguments at the end of a variadic template parameter list. They can be expanded just about anywhere in order to provide a variable list of arguments, either for a function, or for another template instantiation. Despite their power they come with a number of limitations:
- There is no direct way to index or otherwise search the parameters without expanding them.
- There is no direct way to filter the parameters without expanding them.
- You cannot alias or otherwise "hold" a parameter pack around or pass it directly to another template without expanding it.
- You can use a parameter pack to declare a function with as many arguments, but you cannot declare variable numbers of
structorclassmembers using it. - Using them to create functions with variable numbers of arguments basically requires that you create a template function which you call recursively to process each argument in turn, using the recursive iteration technique outlined earlier except for with methods. It's a bit awkward, and not so efficient unless you inline everything and your arguments list is only a few items usually.
- When you declare a function signature by expanding arguments this way, you cannot give the function parameters names.
- Parameter packs must be declared as the last argument to a template
The newest standards have relaxed or removed some of these limitations.
Now that we've covered what you can't do with it, let's cover what you can.
Maybe the most obvious use for a variadic template is a tuple type. Since a tuple can contain an arbitrary number of typed arguments it makes a use case for variadic templates. It should be noted that the STL already contains a tuple class but that wheel will be reinvented here for the purpose of demonstrating how it works:
template<typename...Types>
struct tuple { };This is our bare-bones tuple implementation. It holds no fields, and so it's not very useful on its own. In fact, it doesn't make a lot of sense - what are we doing with the Types parameter pack? The answer is simple: nothing. We're going to specialize the template such that this version only gets instantiated if Types contains no arguments. Hopefully, that makes more sense now.
Parameter Pack "Peeling"
I don't think "peeling" is any kind of official term, but it's the word I use to express the concept of popping or "peeling" the first argument off of a parameter pack argument list, and using it in a template. It's such a common pattern, it deserves a name. This seemed as good as any.
I mentioned that we're going to specialize the above template. In doing so, we will engage in the process of "peeling" arguments off of the parameter pack, and then forwarding what's left to a recursive template instantiation:
template<
// this "peels" the first argument
// from the parameter pack for
// processing here:
typename Type,
// declare a template parameter
// pack:
typename... Types
>
struct tuple<Type, Types...> {
// our current tuple value
Type value;
// here we instantiate a new tuple
// with one fewer argument
tuple<Types...> next;
// we expand the parameter pack into
// arguments to our ctor.
constexpr inline tuple(
const Type& value,
const Types& ... next)
: value(value)
, next(next...) {
}
};I've tried to provide a brief explanation of the different elements of the template above, but it bears further explanation, and maybe an example.
First of all, we have an extra typename argument Type on this template specialization that precedes the parameter pack, Types. This is to facilitate the peeling. I'll explain it how it works:
Say I pass tuple<int, double, char>, which can represent a 3 argument parameter pack, or - get this - a single argument followed by a two argument parameter pack. It's the same thing. The compiler honestly doesn't care, but it will pick the most specialized template first, and that is the single argument parameter Type=int followed by a two argument pack (Types[0]=double, Types[1]=char) in this case. This is how we peel - we create a template that takes a preceding argument which is of the same kind as the arguments in the parameter pack. When the compiler expands the parameter pack, it will expand like (as above) int, double, char. It doesn't care that the template has the first argument as its own parameter. It will pass that particular comma separated list to the template and follow that wherever that leads - even to a template with a single argument of the parameter pack followed by the parameter pack. That's the magic that makes this work.
Here's what the expansion essentially comes out to:
struct tuple_1 {
int value;
struct tuple_2 {
double value;
struct tuple_3 {
char value;
struct tuple_4 {
// from the initial
// empty declaration
} next;
inline constexpr tuple_3(
const char& value1
) : value(value1) {}
} next;
inline constexpr tuple_2(
const double& value1,
const char& value2) :
value(value1),
next(value2) { }
} next;
inline constexpr tuple_1(
const int& value1,
const double& value2,
const char& value3) :
value(value1),
next(value2,value3) { }
};Using Recursion to Process Parameter Packs
Each field of the tuple has its own nested tuple that holds the remaining fields. It's recursion all the way down! Just remember this. It's how you deal with variadic template arguments - recursive instantiation.
To solve a problem involving a variadic template parameter pack, your answer is recursion. In some cases, there are ways to avoid recursion with alternatives, like type inheritance. They accomplish the same thing as recursive techniques but don't whip the compiler so hard. This article isn't about optimizing your compile times, so we won't get into those techniques.
Note that our constructors are inlined and declared with constexpr. Essentially, we don't want them, and we're telling the compiler to eliminate them since they don't help. They're trivial and add nothing to the code except to tell the compiler this can be constructed with a series of typed arguments. Adding a function call to the assignment of the arguments is just overhead, and it doesn't save code space. Furthermore, using constexpr tells the compiler that this constructor is trivial and so it can be instantiated from values all known at compile time, without actually instantiating it in running code. It's basically the second way we tell the compiler to eliminate the constructor, plus we open up the ctor to be used on static const fields, and as a bonus, this tuple can be used entirely at compile time and never placed in running code.
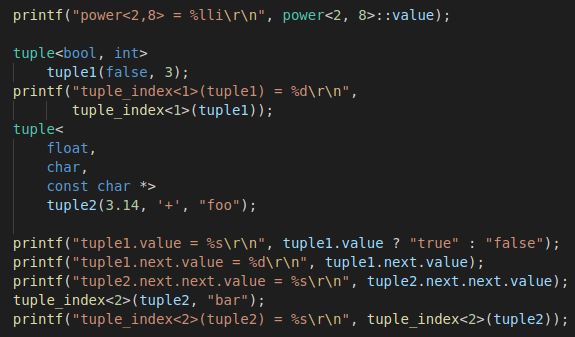
We can use the tuple template like:
tuple<bool,int>
tuple1(false,3);
tuple<
float,
char,
const char*>
tuple2(3.14, '+',"foo");
printf("tuple1.value = %s\r\n",
tuple1.value?"true":"false");
printf("tuple1.next.value = %d\r\n",
tuple1.next.value);
printf("tuple2.next.next.value = %s\r\n",
tuple2.next.next.value);While we can access the fields using a series of next references, that's not exactly convenient. The fields don't have names, so we can't access them that way, but what if we could get them by index?
Indexing Parameter Packs
Now we come to a slightly sticky bit of code - getting a particular argument out of a parameter pack by index.
The concept is easy enough however, mostly because we've done something like it already with the power<X,Y> template from earlier. We start with a particular count - in this case, the desired index, and recursively instantiate the template passing the decremented index until we reach zero by way of a specialization. The only difference from how we did it power<X,Y> is that we're capturing an argument we peel from the template parameter pack as we do so, and of course we have no X parameter we need to multiply.
To demonstrate, we'll start with an admittedly contrived example that nevertheless illustrates the basic idea:
template<
size_t Index,
typename Arg,
typename... Args>
struct arg_by_index {
using type = typename
arg_by_index<Index-1,Args...>::type;
};
template<
typename Arg,
typename... Args>
struct arg_by_index<0,Arg,Args...> {
using type = Arg;
};Here, we have one template, and a specialization of that template for Index=0. You probably noticed the argument pack and the peeling pattern in the template declarations, but notice that there's no template declaration without a leading typename Arg preceding the parameter pack. This is so we don't accept zero arguments after the Index argument.
In the main template declaration, we're creating an alias that recursively instantiates the template with a decremented index, and retrieves the argument - a type referred to as ::type. The specialization for zero will handle retrieving the actual argument, which you can see it does. This should be pretty easy to understand if you've kept up so far.
We use it like this:
printf("sizeof(arg_by_index<1... = %d\r\n",
(int)sizeof(arg_by_index<1,short,char,long>::type));
return 0;
}The above will print 1. This however, is not very useful. Let's look at how to index into our tuple types for something more real world:
// tuple index helper base declaration
template<size_t Index,typename Type>
struct tuple_index_impl {};
// tuple index helper terminator specialization
// on index zero (specialization #1)
template<typename Type, typename... Types>
struct tuple_index_impl<0,tuple<Type,Types...>> {
// indicates the type of the tuple itself
using tuple_type = tuple<Type, Types...>;
// indicates the first value type in the tuple
using value_type = Type;
// retrieve the tuple's value
constexpr inline static value_type value(
tuple_type &t) {
return t.value;
}
// set the tuple's value
constexpr inline static void value(
tuple_type &t,const value_type& v) {
t.value=v;
}
};
// specialization #2 (most used)
template<
size_t Index,
typename Type,
typename... Types
>
struct tuple_index_impl<Index, tuple<Type, Types...>> {
using tuple_type = tuple<Type, Types...>;
using value_type = typename tuple_index_impl<
Index - 1,
tuple<Types...>>::value_type;
constexpr inline static value_type value(
tuple_type &t) {
return tuple_index_impl<
Index - 1,
tuple<Types...>>::value(t.next);
}
constexpr inline static void value(
tuple_type &t,const value_type& v) {
tuple_index_impl<
Index - 1,
tuple<Types...>>::value(t.next,v);
}
};
// static tuple by index getter method template
template<
size_t Index,
typename TupleType
>
typename tuple_index_impl<Index, TupleType>::value_type
tuple_index(TupleType &t) {
return tuple_index_impl<Index, TupleType>::value(t);
}
// static tuple by index setter method template
template<
size_t Index,
typename TupleType
>
void tuple_index(
TupleType &t,
const typename tuple_index_impl<
Index,
TupleType>::value_type& v) {
return tuple_index_impl<Index, TupleType>::value(t,v);
}That's significantly more complicated, but the indexing part is relatively straightforward - it's just that there's a lot more going on as well. Let's go over it.
Consider the following:
tuple<bool,int> tuple1(false,3);
printf("tuple_index<1>(tuple1) = %d\r\n",
tuple_index<1>(tuple1));Here, we request the second item out of the tuple, an int.
This first calls the template function tuple_index<1,tuple<bool,int>>(tuple1). Note the second template argument was actually produced implicitly. The compiler chose it automatically because it can be coerced from the first argument of the function. Even C# coerces arguments for its generic functions this way. It makes code easier to write, and clearer to read, even if it takes a minute to get used to.
Essentially, any time you omit the trailing argument from a template function, it will try to resolve it using the type of the first argument passed to the function. This allows you to kind of "overload" a template function such that it will produce the right template for you based on your passed in argument.
Anyway, the tuple_index() getter declaration, ugly as it is, simply instantiates tuple_index_impl<Index,TupleType> a couple of times* - once to fetch the type of the tuple field at the specified Index which it uses as the return type of the template method, and once to call value(t) to retrieve the current value at the specified index. *Don't worry about instantiating the same template multiple times with the same arguments. A C++ compiler must cache these instantiations such that they all must return the same instantiated type. Therefore, after the first instantiation, further instantiations are simply a lookup into the table of already created types. Normally, you can create an alias in these cases, and simply refer to that, but with the above, I didn't feel justified in polluting the namespace with an additional name that would only be used here.
Now let's tackle the core of this - the tuple_index_impl<> template. For a non-empty tuple, with a non-zero Index the compiler will choose specialization #2. With tuple_index<1>(tuple1) it would choose this second specialization of the above template.
In that specialization, it captures the type of the current tuple passed in - remember that each tuple is actually a value and a nested tuple with each remaining field - in tuple_type. More importantly, the value_type alias recursively instantiates tuple_index_impl<> passing a decremented Index all the way down to specialization #1. This should seem familiar, since we've now done this before more than once.
The template declares two value() method overloads for the main specializations. These get and set the values. Note that the second specialization recursively calls down until it hits the first specialization at Index zero, just like we did with value_type. All these functions are inlined because they don't add anything to running code - they don't save any space by including them since they are trivial. The only thing they are needed for is to guide the compiler to generate the right mov instruction at the right offset. After that, they can be tossed, rather than incurring the overhead of creating a stack frame and then calling that mov instruction, and then destroying that stack frame.
Now that we've unpacked what it's doing, I think we can move on to a final trick - attaching strings to templates and then matching on them at compile time.
String Theory
You can't directly pass strings as template arguments. Your compiler will yell at you, and that's no fun for anyone. However, just because you can't do something doesn't mean you can't do something. This is C++, after all. All "you can't do that" really means in C++ is "sure you can do it, if you're willing to do questionable things to your compiler and your codebase."
Here, we're going to relax the limitation on passing strings to templates, and we'll do so by wrapping strings in types, and pass those types to templates. The following should make it clear:
#define STRING(x) \
struct { \
constexpr static inline const char \
*value() { return x; } \
};You can declare a string like:
using foo = STRING("foo");You can take it in a template like:
template<typename String>
static void print_str() {
printf("%s",String::value());
}
print_str<foo>(); // prints "foo"This isn't all that clever, but it's a starting point. What we'd like to do really, is match on strings during compile time. If we could do that, then we could attach a string key, or name onto each type we pass to variadic template, and then search through those variadic arguments for a matching string, returning the associated argument.
Let's simplify the problem with a first step - getting the index of a string argument from a variadic template. First, with the initial template declaration:
// helper that fetches the index of a string
template <size_t Index,
typename Match,
typename... Strings>
struct index_of_string_impl;Here, we're taking an Index that we use to count indices, a Match typename that holds our "string" type, and finally a list of "strings". Now we need a version that doesn't take any strings. We use this one to represent the "not found" condition:
template <size_t Index, typename Match>
struct index_of_string_impl<Index, Match> {
// this is what we return when it's
// not found
static constexpr size_t value = -1;
};Now onto the real meat of it - the general case:
template <size_t Index,
typename Match,
typename String,
typename... Strings>
struct index_of_string_impl<
Index,
Match,
String,
Strings...> {
static constexpr size_t value = is_same<Match, String>::value ?
// if it's a match return the current Index,
Index
:
// if it's not a match, instantiate the next
// template in the series with an incremented
// Index, and the remaining Strings, and then
// fetch it's value. This will wind up being
// the matched index, or -1 depending if the
// Match is found or not
index_of_string_impl<Index + 1,
Match,
Strings...>::value;
};The comments should hopefully make most of it clear. Basically, we're just peeling and counting recursively, until is_same<>::value winds up true, but what is is_same<> doing?
The is_same<> template is provided by the STL, but we'll revisit it here so you can understand it:
// represents a boolean type
// std has this
template <bool Value>
struct boolean_type {
constexpr static const bool value = Value;
};
// indicates whether or not two types are the same
// std has this
template <typename T, typename U>
struct is_same : boolean_type<false> {};
// specialization of is_same:
template <typename T>
struct is_same<T, T> : boolean_type<true>{};I'm not going to sit here and tell you that this is the implementation the STL uses. It's almost certainly not, but it is a functionally equivalent implementation, and that's what matters. The boolean_type<> template is just a slightly more flexible way to represent a boolean value. It wasn't necessary here. We could have simply put a bool value field on is_same<> itself. The STL does something more like the above code though, so I wanted to illustrate it in case you run into it in the wild.
The interesting part here is the specialization of is_same<>. The compiler is clever enough to choose it when you pass the same type in as both the first and second argument, due to is_same<T,T>. In the earlier function, we used it to determine if the passed in "string" type was the same as the one in the argument list.
Finally, we simply wrap the index_of_string_impl<> helper with something friendlier:
template <typename Match, typename... Strings>
using index_of_string =
index_of_string_impl<0, Match, Strings...>;We can then use it like this:
using foobar_str = STRING("foobar");
using foo_str = STRING("foo");
using baz_str = STRING("baz");
printf("index of \"%s\" within string list: %d\r\n",
foobar_str::value(),
(int)index_of_string<
foo_str, // match arg
foobar_str, // string #1
foo_str, // string #2
baz_str // string #3
>::value);You may have noticed this works by comparing types, not strings. The truth is there's a glaring limitation with this technique - you can't simply match on an arbitrary string. For example, the following will not return the intuitive result:
using match = STRING("foobar");
using foobar_str = STRING("foobar");
using foo_str = STRING("foo");
using baz_str = STRING("baz");
printf("index of \"%s\" within string list: %d\r\n",
foobar_str::value(),
(int)index_of_string<
match, // match arg
foobar_str, // string #1
foo_str, // string #2
baz_str // string #3
>::value);That will return -1 because the match type does not exist in the list. It doesn't actually care about the string it contains, or that it happens to match the string in foobar_str. It only cares about the type. There's no real way around this in C++11 at compile time, but it's still useful. Consider the situation where you have a list of well known strings. We'll use colors as an example:
// an ersatz "enum" that holds types
struct color_name {
using white = STRING("white");
using black = STRING("black");
using red = STRING("red");
using green = STRING("green");
using yellow = STRING("yellow");
using purple = STRING("purple");
using blue = STRING("blue");
using cyan = STRING("cyan");
};Now we'll go ahead and make some complementary declarations, one for a color_traits template that will represent a color value, and another pseudo-"enum", color to hold the well known ones as we did above:
template<
typename Name,
unsigned char Red,
unsigned char Green,
unsigned char Blue
>
struct color_traits {
using name_type = Name;
constexpr inline static const char* name() {
return Name::value();
}
constexpr static const unsigned char red = Red;
constexpr static const unsigned char green = Green;
constexpr static const unsigned char blue = Blue;
constexpr static const unsigned long int value =
(red<<16)|(green<<8)|blue;
};
struct color {
using white = color_traits<color_name::white,
0xFF,0xFF,0xFF>;
using black = color_traits<color_name::black,
0x00,0x00,0x00>;
using red = color_traits<color_name::red,
0xFF,0x00,0x00>;
using green = color_traits<color_name::green,
0x00,0xFF,0x00>;
using yellow = color_traits<color_name::yellow,
0xFF,0xFF,0x00>;
using purple = color_traits<color_name::purple,
0xFF,0x00,0xFF>;
using blue = color_traits<color_name::blue,
0x00,0x00,0XFF>;
using cyan = color_traits<color_name::cyan,
0x00,0xFF,0XFF>;
};You'll note that a color_traits instantiation has a name, and red, green, and blue color channel values associated with it. You're probably wondering why we have a name at all, but continue to bear with me as we do more declarations and it will become clear:
template<typename... ColorTraits>
struct palette {
using type = palette<ColorTraits...>;
constexpr static const int size = sizeof...(ColorTraits);
};Now we can declare:
using french_flag_palette =
palette<
color::blue,
color::white,
color::red
>;
// the Americans, just to be Americans,
// decide to use our own color of blue,
// which we also call "blue", but is
// slightly darker, because 'murica
using usa_flag_palette =
palette<
color::red,
color::white,
color_traits<
color_name::blue,
0,0,0xE0>
>;We've declared two palettes of red, white and blue for two different flags. The French colors appear in a different order than the USA colors, and the USA's "blue" color is slightly darker, but we still call it blue, just like we still call American football football. Because who is going to stop us? Either way, both flags have white, blue and red colors in them.
Now we'd like to do:
printf("French flag color at index one is: %s\r\n",
french_flag_palette::color_by_index<1>::name());That's easy enough based on what we've already learned. We just need to retrieve an argument from a parameter pack by index. Watch:
template<size_t Index,
typename ColorTrait,
typename... ColorTraits>
struct color_by_index_impl {
using color = typename
color_by_index_impl<Index-1,ColorTraits...>::color;
};
template<typename ColorTrait,
typename ... ColorTraits>
struct color_by_index_impl<0,ColorTrait,ColorTraits...> {
using color = ColorTrait;
};That helper template and specialization now allows us from inside the palette class template to declare a using for color_by_index<>:
template<typename... ColorTraits>
struct palette {
...
template<size_t Index>
using color_by_index = typename
color_by_index_impl<Index,ColorTraits...>::color;
...
};Now, for something more meaty, let's get a color index by name:
// will print 2
printf("USA flag palette blue index is %d\r\n",
(int)usa_flag_palette::color_index_by_name<color_name::blue>::value);Finally, the use for having a name might be clicking for you. Basically, we can treat it like a tag to identify a type. Keep in mind there are two different blue colors in play, one on the French flag and one on the USA flag. Searching by color_name::blue will return either one.
Now for the templates that enable color_index_by_name<>:
// helper that fetches the index of a color by name
template <size_t Index,
typename Match,
typename... ColorTraits>
struct color_index_by_name_impl;
template <size_t Index, typename Match>
struct color_index_by_name_impl<Index, Match> {
// this is what we return when it's
// not found
static constexpr size_t value = -1;
};
// this is the meat of color_index_by_name_impl:
template <size_t Index,
typename Match,
typename ColorTrait,
typename... ColorTraits>
struct color_index_by_name_impl<
Index,
Match,
ColorTrait,
ColorTraits...> {
static constexpr size_t value = is_same<Match, typename ColorTrait::name_type>::value ?
Index
:
color_index_by_name_impl<Index + 1,
Match,
ColorTraits...>::value;
};This was very nearly cut and paste from the code for searching a string list, so I won't spend a lot of time going over it. Now like before, we just alias a member onto the palette template class that invokes this helper:
template<typename... ColorTraits>
struct palette {
...
// from before:
template<size_t Index>
using color_by_index = typename color_by_index_impl<Index,ColorTraits...>::color;
template<typename Name>
using color_index_by_name = color_index_by_name_impl<0,Name,ColorTraits...>;
// free bonus member:
template<typename Name>
using color_by_name = color_by_index<color_index_by_name<Name>::value>;
...
};Here, we've simply "wrapped" the template instantiation with a using template as before, and as a bonus we've added the color_by_name member which retrieves a color_trait type given a name.
Now, hang on to your hat.
Game, Set and Match
We're going to use pretty much everything we've covered for one final push - set computations.
We're going to implement a subset/superset, equals, and unordered equals comparison for palettes, which match on the color names, all at compile time.
It's actually pretty easy now that we've done all of the above, but just think of the work that you can make the compiler do with techniques like this.
The superset/subset implementation is the simplest:
template <typename PaletteType, typename...ColorTraits>
struct is_subset_palette_impl;
template <typename PaletteType>
struct is_subset_palette_impl<PaletteType> {
// this is what we return when there
// are no items left
static constexpr bool value = true;
};
template <typename PaletteType,
typename ColorTrait,
typename... ColorTraits>
class is_subset_palette_impl<
PaletteType,
ColorTrait,
ColorTraits...> {
using result = typename PaletteType::color_index_by_name<typename ColorTrait::name_type>;
using next = typename ::is_subset_palette_impl<PaletteType,ColorTraits...>;
public:
static constexpr bool value = (-1!=result::value) &&
next::value;
};It might be weird that we have a couple of private members, but the truth is I needed some "scratch" fields to hold intermediary instantiations because the C++ compiler was having trouble parsing everything inline. I didn't have to make them private, but I felt like it was better to hide them since they serve no purpose other than to cajole the compiler into digesting a piece of code I gave it. Here, next is the operative instantiation - the one that recurses, checking each member of ColorTraits in turn. result is also important, since it retrieves the index of the color by name from the other palette. We check it against -1 to see if the color exists, and also check that the next value is also true. When there are no more ColorTraits arguments, we return "true" as the final value in the boolean && operator chain.
Now as before, we create an alias member on palette that invokes the above:
template<typename PaletteOther>
using is_superset_of = is_subset_palette_impl<PaletteOther,ColorTraits...>;
template<typename PaletteOther>
using is_subset_of = typename PaletteOther::is_superset_of<type>;I didn't paste the surrounding palette template class definition like before but you get the idea.
Now to build on that, we can do an unordered equals, which ultimately just involves doing is_superset_of<> in both directions:
template <typename PaletteTypeLhs,typename PaletteTypeRhs>
class unordered_equals_palette_impl {
using lhs = typename PaletteTypeLhs::is_superset_of<PaletteTypeRhs>;
using rhs = typename PaletteTypeRhs::is_superset_of<PaletteTypeLhs>;
public:
constexpr static bool value = lhs::value &&
rhs::value;
};There are those private members again. This time, it was just to keep the code readable.
Finally, we have the alias in the palette template class:
template<typename PaletteOther>
using unordered_equals = unordered_equals_palette_impl<type,PaletteOther>;Now we can do things like:
// returns true
printf("French palette is superset of USA palette = %s\r\n",
french_flag_palette::is_superset_of<usa_flag_palette>::value?"true":"false");
// returns true
printf("Unordered equals, French vs USA palettes = %s\r\n",
usa_flag_palette::unordered_equals<french_flag_palette>::value?"true":"false");Neat, but now what about ordered equality? You might think that's an easier nut to crack than unordered equality but there's a wrinkle. Traditionally, you'd walk through both sets at the same time comparing each item at each index, assuming the counts were the same, and return true if everything is true. However, there's not a straightforward way to unpack two sets of parameter packs at the same time, so you can't easily walk two sets like this.
What I ended up doing was modifying the is_subset_palette_impl<> to create a version that compares the indices of items to make sure they match, rather than just returning true if it's not -1. It's a lot more work for the compiler, but whatever. I'm not here to make friends with the compiler:
template <
typename PaletteType,
size_t Index,
typename...ColorTraits>
struct is_equal_palette_impl;
template <
typename PaletteType,
size_t Index>
struct is_equal_palette_impl<PaletteType,Index> {
// this is what we return when there
// are no items left
static constexpr bool value = true;
};
template <typename PaletteType,
size_t Index,
typename ColorTrait,
typename... ColorTraits>
class is_equal_palette_impl<
PaletteType,
Index,
ColorTrait,
ColorTraits...> {
using result = typename
PaletteType::color_index_by_name<typename ColorTrait::name_type>;
using next = typename
::is_equal_palette_impl<PaletteType,Index+1,ColorTraits...>;
public:
static constexpr bool value = result::value==Index && next::value;
};
template <typename PaletteTypeLhs,typename... ColorTraits>
class equals_palette_impl {
using compare = typename
::is_equal_palette_impl<PaletteTypeLhs,0,ColorTraits...>;
public:
constexpr static bool value =
PaletteTypeLhs::size==sizeof...(ColorTraits) &&
compare::value;
};Index here is used to count from zero. That way, we keep track of our index into the first list, which we compare with the index we get back from the result of color_index_by_name<>. We only return true if they match.
Naturally, we add an alias to palette:
template<typename PaletteOther>
using equals = equals_palette_impl<PaletteOther,ColorTraits...>;We use it like this:
// returns false
printf("Ordered equals, French vs USA palettes = %s\r\n",
usa_flag_palette::equals<french_flag_palette>::value?"true":"false");The complete palette template looks like this:
template<typename... ColorTraits>
struct palette {
using type = palette<ColorTraits...>;
constexpr static const int size = sizeof...(ColorTraits);
template<size_t Index>
using color_by_index = typename color_by_index_impl<Index,ColorTraits...>::color;
template<typename Name>
using color_index_by_name = color_index_by_name_impl<0,Name,ColorTraits...>;
template<typename Name>
using color_by_name = color_by_index<color_index_by_name<Name>::value>;
template<typename PaletteOther>
using is_superset_of = is_subset_palette_impl<PaletteOther,ColorTraits...>;
template<typename PaletteOther>
using is_subset_of = typename PaletteOther::is_superset_of<type>;
template<typename PaletteOther>
using unordered_equals = unordered_equals_palette_impl<type,PaletteOther>;
template<typename PaletteOther>
using equals = equals_palette_impl<PaletteOther,ColorTraits...>;
};Like I said before, it's a little contrived, but it doesn't take much imagination to figure out where you can use these techniques to make your own code more flexible and/or efficient.
Don't get discouraged trying to solve problems this way. I'd be embarrassed to tell you how long some of the simpler techniques here took me to develop. It really does require you to attack problems sideways rather than head on, but it gets easier with practice. The best way to get practice is to simply try.
I like to think of these problems as puzzle games, and it helps make it more fun than frustrating. It doesn't always work, but like I said, it helps.
History
- 23rd March, 2021 - Initial submission