Visual FA Part 3: The Code Behind It All
Updated on 2024-01-20
In this article, we explore the inner workings of Visual FA
Introduction
Article list
Note: Understanding the concepts in Part 1 will be critical for this article. Part 2 is also helpful so you can understand what we're dealing with, but Part 1 is absolutely essential. Some of the code in the article may be slightly out of date, as the codebase has been updated since this was written.
Well, I promised we'd get here. I'm a bit overwhelmed and not sure where to begin. That's a perfect time to start writing!
So far, we've gone over finite automata concepts, and usage of the API. Now let's dive into the code. We'll be focusing on the FA class in this article since everything else revolves around this class.
Transitions and Other Core Members
We'll begin with the basics - managing the core automata functionality, which means dealing with transitions and basics like the accept symbol.
A valid AcceptSymbol must be non-negative, so we have an IsAccepting property to check that. Despite its importance, the implementation isn't exciting. It's also trivial, consisting of a field mapping in one case, and an if check on that field in the case of the other member. Simple.
Let's consider our transitions. That's where the meat of the data is. We keep a list of them internally in the _transitions member. Here's the declaration for FATransition:
struct FATransition
{
public int Min;
public int Max;
public FA To;
public FATransition(FA to, int min = -1, int max =-1)
{
Min = min;
Max = max;
To = to;
}
public bool IsEpsilon { get { return Min == -1 && Max == -1; } }
public override string ToString()
{
if(IsEpsilon)
{
return string.Concat("-> ", To.ToString());
}
if (Min == Max)
{
return string.Concat("[",
char.ConvertFromUtf32(Min),
"]-> ",
To.ToString());
}
return string.Concat("[",
char.ConvertFromUtf32(Min),
"-",
char.ConvertFromUtf32(Max),
"]-> ",
To.ToString());
}
public bool Equals(FATransition rhs)
{
return To == rhs.To &&
Min == rhs.Min &&
Max == rhs.Max;
}
public override int GetHashCode()
{
if(To==null)
{
return Min.GetHashCode() ^
Max.GetHashCode();
}
return Min.GetHashCode() ^
Max.GetHashCode() ^
To.GetHashCode();
}
public override bool Equals(object obj)
{
if (ReferenceEquals(obj, null)) return false;
if (!(obj is FATransition)) return false;
FATransition rhs = (FATransition) obj;
return To == rhs.To && Min == rhs.Min && Max == rhs.Max;
}
}It's pretty simple. Basically, it either holds a range of codepoints indicated by Min and Max, or it is an epsilon transition in which case both of those fields are -1. The reason we use ranges is due to Unicode making it impractical in many situations to store single codepoints. There are whole blocks of related codepoints that are best represented using ranges. In any case, FATransition also holds a reference to the destination state in To*. It implements value equality semantics for reasons we'll explore later. Note that we don't use properties for the primary members. The dirty truth is I don't trust the JIT compiler to resolve those to access the fields directly, and they are too time critical to incur the overhead of a getter method call.
Anyway, we keep a list sorted on insert called _transitions on FA. Note I didn't make FATransition implement IComparable
*Astute developers might realize there's a situation with looping transitions where it will cause undue strain on the garbage collector due to circular references, however indirect. In practice, the GC seems to handle it fine, and I can't use WeakReference
On FA, the user can retrieve a read only list of transitions using the Transitions property. The property simply returns _transitions.AsReadOnly(). The reason I didn't cache it is that it is rarely used so it didn't seem worth incurring even a little bit of extra memory on each FA instance to hold something that may never get called on.
We have transitions, great. Now we need a way to add them. FA provides two members for doing that - AddTransition() and AddEpsilon(). We do a bit of preprocessing on each. For starters, we do sorted inserts. Secondly, we do duplicate elimination. Finally, we do overlap checking (using FARange) in AddTransition(), and in both cases, we update IsDeterministic and/or IsCompact as necessary.
I thought about adding a FATransitionsList specialization that had an Add() method on it that would do all of this, but it would be extra indirection and thus extra overhead and extra memory without really adding much other than fluff.
Anyway, here's AddTransition():
public void AddTransition(FARange range,FA to)
{
if (to == null)
throw new ArgumentNullException(nameof(to));
if(range.Min==-1 && range.Max==-1)
{
AddEpsilon(to);
return;
}
if(range.Min>range.Max)
{
int tmp = range.Min;
range.Min = range.Max;
range.Max = tmp;
}
var insert = -1;
for (int i = 0; i < _transitions.Count; ++i)
{
var fat = _transitions[i];
if (to == fat.To)
{
if(range.Min==fat.Min &&
range.Max==fat.Max)
{
return;
}
}
if (IsDeterministic)
{
if (range.Intersects(
new FARange(fat.Min, fat.Max)))
{
IsDeterministic = false;
}
}
if (range.Max>fat.Max)
{
insert = i;
}
if (!IsDeterministic &&
range.Max < fat.Min)
{
break;
}
}
_transitions.Insert(insert+1,
new FATransition(to, range.Min, range.Max));
}AddEpsilon() does a bit of fancy footwork if you compact. It "cheats" but in a way that is mathematically acceptable. Basically, instead of adding an additional state when you add an epsilon, you merge the new state with the existing state. This effectively accomplishes the same thing as if you were doing epsilon closures, but without the overhead. Furthermore, in many cases, these compact creations are also deterministic! That means you will enjoy optimized traversal without additional overhead of creating a DFA, although the result won't be minimized. This only applies to states without conflicting transitions, but that covers scenarios like foo|bar. Anyway, here it is:
public void AddEpsilon(FA to, bool compact = true)
{
if(to==null) throw new ArgumentNullException(nameof(to));
if (compact)
{
for (int i = 0; i < to._transitions.Count; ++i)
{
var fat = to._transitions[i];
if (fat.Min!=-1 || fat.Max!=-1)
{
AddTransition(new FARange(fat.Min, fat.Max), fat.To);
}
else
{
AddEpsilon(fat.To, true);
}
}
if (AcceptSymbol < 0 && to.AcceptSymbol > -1)
{
AcceptSymbol = to.AcceptSymbol;
}
}
else
{
var found =false;
int i;
for (i = 0;i<_transitions.Count;++i)
{
var fat = _transitions[i];
// this is why we don't use List.Contains:
if (fat.Min != -1 || fat.Max != -1) break;
if(fat.To==to)
{
found = true;
break;
}
}
if (!found)
{
_transitions.Insert(i,new FATransition(to));
IsCompact = false;
IsDeterministic = false;
}
}
}Thompson Construction Algorithms
Of course, we rarely use these methods above directly. Instead, we have methods that build basic constructs using these methods above - the Thompson construction methods, plus some related convenience methods I've augmented that canonical suite with. They include Literal(), Set(), Concat(), Or(), Optional(), Repeat() and CaseInsensitive().
Literal builds things like this (Literal("ABC")) like we covered in the first article:

public static FA Literal(IEnumerable<int> codepoints, int accept = 0, bool compact = true)
{
var result = new FA(accept);
var current = result;
foreach (var codepoint in codepoints)
{
// remove the previous accept
current.AcceptSymbol = -1;
// new state is accepting
var fa = new FA(accept);
current.AddTransition(new FARange(codepoint, codepoint), fa);
current = fa;
}
return result;
}
public static FA Literal(string @string, int accept = 0, bool compact = true)
{
return Literal(ToUtf32(@string), accept, compact);
}Note that our methods typically deal in UTF-32 codepoints as ints. There is a ToUtf32() method that converts strings or char arrays. It's used above.
Next up, we have Set() which builds constructs like this:
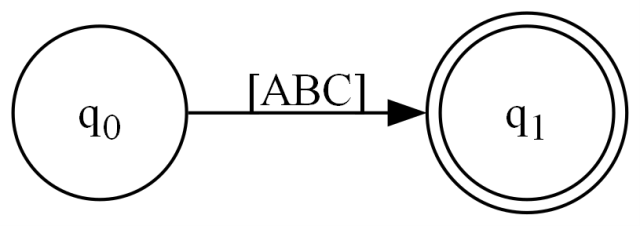
This implementation is dead simple since all we're doing is adding transitions to a single state. I used to sort ranges here, but don't have to anymore, since that's handled by AddTransition().
public static FA Set(IEnumerable<FARange> ranges, int accept = 0, bool compact = true)
{
var result = new FA();
var final = new FA(accept);
foreach (var range in ranges)
result.AddTransition(range, final);
return result;
}That covers are sort of "atomic" functions. The rest operate on other state machines, basically cloning whatever's passed in, modifying that accordingly and then returning it. None of these functions change the original expression. It's less performant this way, but much safer API-wise. Down the road, I may make internal functions that do not clone the states, which would be used by other methods like Parse().
Anyway, next we'll cover concatenation:

public static FA Concat(IEnumerable<FA> exprs, int accept = 0, bool compact = true)
{
FA result = null, left = null, right = null;
// we need to break the expressions into left and right
// pairs to pass to _Concat. There are several corner
// cases to consider, such as having one expression
// or no expressions.
foreach (var val in exprs)
{
if (null == val) continue;
var nval = val.Clone();
if (null == left)
{
if (null == result)
result = nval;
left = nval;
continue;
}
if (null == right)
{
right = nval;
}
nval = right.Clone();
_Concat(left, nval, compact);
right = null;
left = nval;
}
// we need to handle the tail where _Concat didn't.
// find all accept states and set the value to
// the "accept" arg
if (null != right)
{
var acc = right.FillFind(AcceptingFilter);
for (int ic = acc.Count, i = 0; i < ic; ++i)
acc[i].AcceptSymbol = accept;
}
else
{
var acc = result.FillFind(AcceptingFilter);
for (int ic = acc.Count, i = 0; i < ic; ++i)
acc[i].AcceptSymbol = accept;
}
// if no expressions we don't accept anything
return result==null?new FA():result;
}
static void _Concat(FA lhs, FA rhs, bool compact)
{
// take the left hand, clear all the accept states
// and then add an epsilon from each to the start
// of the right hand
var acc = lhs.FillFind(AcceptingFilter);
for (int ic = acc.Count, i = 0; i < ic; ++i)
{
var f = acc[i];
f.AcceptSymbol = -1;
f.AddEpsilon(rhs, compact);
}
}Here _Concat() does the actual concatenation between two machines, but Concat() takes a list of machines and turns them into pairs of machines, mindful of the weird cases, as well as finalizing the accepting states.
Now we have Or() which creates a dysjunction/choice between one machine and another:
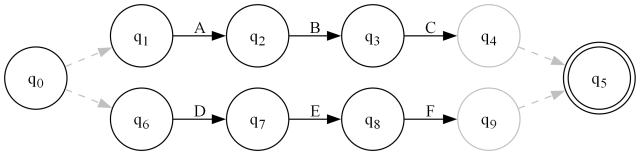
public static FA Or(IEnumerable<FA> exprs, int accept = 0, bool compact = true)
{
var result = new FA();
var final = new FA(accept);
// for each expr
// 1. add an epsilon from result to the expr
// 2. set all the accept states to non-accepting
// 3. add an epsilon from each to the final state
// unless the state is null in which case
// we just add an empty transition to the final
// state making the whole expression optional so
// (foo|bar|) works as expected
foreach (var fa in exprs)
{
if (null != fa)
{
var nfa = fa.Clone();
result.AddEpsilon(nfa, compact);
var acc = nfa.FillFind(AcceptingFilter);
for (int ic = acc.Count, i = 0; i < ic; ++i)
{
var nffa = acc[i];
nffa.AcceptSymbol = -1;
nffa.AddEpsilon(final, compact);
}
}
else result.AddEpsilon(final, compact);
}
return result;
}The comments and figure should make the above pretty clear, as this is a straightforward construction.
Moving on, we have Optional() which simply makes an expression or the empty string accept:
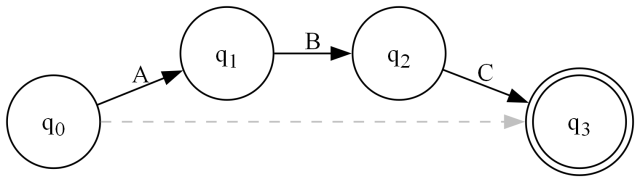
public static FA Optional(FA expr, int accept = 0, bool compact = true)
{
var result = expr.Clone();
if(result.IsAccepting) return result;
// get all the accept states
var acc = result.FillFind(AcceptingFilter);
FA final = null;
if(acc.Count>1)
{
// there's more than one. we have to first
// funnel all of them to one single accept
final = new FA(accept);
for (int ic = acc.Count, i = 0; i < ic; ++i)
{
var fa = acc[i];
fa.AcceptSymbol = -1;
fa.AddEpsilon(final, compact);
}
} else
{
// just change the accept symbol to the final one.
final = acc[0];
final.AcceptSymbol = accept;
}
// bridge the first state to the last one.
result.AddEpsilon(final, compact);
return result;
}This one should be easy, but I found a bug in it this morning in the case of multiple accept states. I now handle that separately above. I may handle it differently in the future, as there's an alternative that doesn't collapse accept states, but I'm hesitant to mess with something working.
The next one is probably the most complicated. It uses itself as well as other construction methods to fulfill the operation it's given.
I can't graph all the different scenarios here. The simplest ones are basic loop constructs like the following:
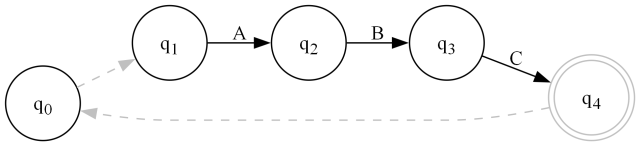
That's FA.Repeat(FA.Literal("ABC"),1) or (ABC)+. A similar construction FA.Repeat(FA.Literal("ABC")) or (ABC)* would be the same except q0 would contain an epsilon the other direction q0->q4 as well as q4->q0.
Another situation is when you have more than one minimum occurrence. Consider FA.Repeat(FA.Literal("ABC"),3,3) or (ABC){3,3}:

It simply creates 2 additional copies of the expression (for 3 total).
Now consider: FA.Repeat(FA.Literal("ABC"),2,3) or (ABC){2,3}:

It's long, it's ugly, and it's deep:
public static FA Repeat(FA expr,
int minOccurs = 0,
int maxOccurs = 0,
int accept = 0,
bool compact = true)
{
if (minOccurs < 0) minOccurs = 0;
if (maxOccurs < 0) maxOccurs = 0;
expr = expr.Clone();
if (minOccurs > 0 && maxOccurs > 0 && minOccurs > maxOccurs)
throw new ArgumentOutOfRangeException(nameof(maxOccurs));
FA result;
switch (minOccurs)
{
case 0: // lower bound unbounded. whole expression is optional
switch (maxOccurs)
{
case 0:
result = new FA(accept);
result.AddEpsilon(expr, compact);
foreach (var afa in expr.FillFind(AcceptingFilter))
{
afa.AddEpsilon(result, compact);
}
return result;
case 1:
result = Optional(expr, accept, compact);
return result;
default:
var l = new List<FA>();
expr = Optional(expr, accept, compact);
l.Add(expr);
for (int i = 1; i < maxOccurs; ++i)
{
l.Add(expr.Clone());
}
result = Concat(l, accept, compact);
return result;
}
case 1:
switch (maxOccurs)
{
case 0:
result = Repeat(expr, 0, 0, accept, compact);
result.AcceptSymbol = -1;
return result;
case 1:
return expr;
default:
result = Concat(
new FA[] { expr,
Repeat(expr,
0,
maxOccurs - 1,
accept,
compact) },
accept,
compact);
return result;
}
default:
switch (maxOccurs)
{
case 0:
result = Concat(
new FA[] {
Repeat(expr,
minOccurs,
minOccurs,
accept,
compact),
Repeat(expr,
0,
0,
accept,
compact) },
accept,
compact);
return result;
case 1:
throw new ArgumentOutOfRangeException(nameof(maxOccurs));
default:
if (minOccurs == maxOccurs)
{
var l = new List<FA>();
l.Add(expr);
for (int i = 1; i < minOccurs; ++i)
{
var e = expr.Clone();
l.Add(e);
}
result = Concat(l, accept);
return result;
}
result = Concat(new FA[] {
Repeat(
expr,
minOccurs,
minOccurs,
accept,
compact),
Repeat(
Optional(
expr,
accept,
compact),
maxOccurs - minOccurs,
maxOccurs - minOccurs,
accept,
compact) },
accept,
compact);
return result;
}
}
}Finally, we CaseInsenstive() which will make a machine ignore character case. This isn't really a Thompson algorithm but it's of a kind, so I include it.

public static FA CaseInsensitive(FA expr)
{
const string emsg = "Attempt to make an invalid range case insensitive";
var result = expr.Clone();
var closure = new List<FA>();
result.FillClosure(closure);
for (int ic = closure.Count, i = 0; i < ic; ++i)
{
var fa = closure[i];
var t = new List<FATransition>(fa._transitions);
fa.ClearTransitions();
foreach (var trns in t)
{
var f = char.ConvertFromUtf32(trns.Min);
var l = char.ConvertFromUtf32(trns.Max);
if (char.IsLower(f, 0))
{
if (!char.IsLower(l, 0))
throw new NotSupportedException(emsg);
fa.AddTransition(new FARange(
trns.Min,
trns.Max),
trns.To);
f = f.ToUpperInvariant();
l = l.ToUpperInvariant();
fa.AddTransition(new FARange(
char.ConvertToUtf32(f, 0),
char.ConvertToUtf32(l, 0)),
trns.To);
}
else if (char.IsUpper(f, 0))
{
if (!char.IsUpper(l, 0))
throw new NotSupportedException(emsg);
fa.AddTransition(new FARange(trns.Min, trns.Max), trns.To);
f = f.ToLowerInvariant();
l = l.ToLowerInvariant();
fa.AddTransition(new FARange(
char.ConvertToUtf32(f, 0),
char.ConvertToUtf32(l, 0)),
trns.To);
}
else
{
fa.AddTransition(new FARange(
trns.Min,
trns.Max),
trns.To);
}
}
}
return result;
}What we're doing here is simply looking for letters and then adding the alternative casing for each one. If we encounter a range with one letter and one non-letter we error, but in practice I've never seen that.
Finding States
Normally, when you reference a state machine with Visual FA, you do so by using q0 as a handle to the whole machine. If you need a list of all the states in the machine, you take the closure of q0. We have FillClosure() for that:
void _Closure(IList<FA> result)
{
if (!_Seen.Add(this))
{
return;
}
result.Add(this);
for (int ic = _transitions.Count, i = 0; i < ic; ++i)
{
var t = _transitions[i];
t.To._Closure(result);
}
}
public IList<FA> FillClosure(IList<FA> result = null)
{
if (null == result)
result = new List<FA>();
_Seen.Clear();
_Closure(result);
return result;
}Essentially, we're recursively checking all transitions from states we haven't seen yet and adding their destination to the result. _Seen is a thread static HashSet
We've covered this before, but it's worth repeating that the FillXXXX() APIs allow you to optionally recycle lists whereas a GetXXXX() style API that simply returned a list would not. This is for performance.
There's a similar operation - taking the epsilon closure - that finds all states reachable from a given state or states only along epsilon transitions. You can perform it with FillEpsilonClosure(). It may seem inconsistent that unlike FillClosure() these methods are static. The reason is related to the fact that this operation is most often done on a list of states rather than just one. It has to do with a limitation of C# (and most similar languages actually) where the compiler can't disambiguate the result from the fill method with the initial states parameter on the necessary static version, so both overloads are static. Anyway, here they are:
IList<FA> _EpsilonClosure(IList<FA> result, HashSet<FA> seen)
{
if(!seen.Add(this))
{
return result;
}
result.Add(this);
if(IsCompact)
{
return result;
}
for (int i = 0; i < _transitions.Count; ++i)
{
var t = _transitions[i];
if(t.Min==-1 && t.Max==-1)
{
if (t.To.IsCompact)
{
if (seen.Add(t.To))
{
result.Add(t.To);
}
}
else
{
t.To._EpsilonClosure(result, seen);
}
} else {
// no more epsilons. we're done
break;
}
}
return result;
}
public static IList<FA> FillEpsilonClosure(IList<FA> states,
IList<FA> result=null)
{
if (null == result)
result = new List<FA>();
_Seen.Clear();
for(int i = 0;i<states.Count;++i)
{
var fa = states[i];
fa._EpsilonClosure(result,_Seen);
}
return result;
}
public static IList<FA> FillEpsilonClosure(FA state,
IList<FA> result = null)
{
if (null == result)
result = new List<FA>();
_Seen.Clear();
state._EpsilonClosure(result, _Seen);
return result;
}This is pretty much the same as FillClosure() in terms of how it operates except that it only cares about epsilon transitions and there's an overload that works with multiple states. Note that when hunting for epsilon transitions, we exit early if we find one that's not epsilon. This is because epsilon transitions are always inserted first in the _transitions list so if we find one that's not epsilon we've already seen them all.
Note: The API immediately below will probably be modified soon to add more information to the FAFindFilter delegate:
void _Find(FAFindFilter filter,
IList<FA> result)
{
if (!_Seen.Add(this))
{
return;
}
if (filter(this))
{
result.Add(this);
}
for (int i = 0; i < _transitions.Count; ++i)
{
var t = _transitions[i];
t.To._Find(filter, result);
}
}
public IList<FA> FillFind(FAFindFilter filter,
IList<FA> result = null)
{
if (null == result)
result = new List<FA>();
_Seen.Clear();
_Find(filter, result);
return result;
}You might note that we can't take any kind of closure from within an FAFindFilter call because of the use of _Seen in these methods. I'm strongly considering creating a separate thread static hash set for this. Anyway, what it does is fairly straightforward. It follows all transitions and for any unseen states, it calls FAFindFilter. If that returns true, it adds it to the result.
FindFirst() is a related method that finds only the first occurence and then stops looking:
FA _FindFirst(FAFindFilter filter)
{
if (!_Seen.Add(this))
{
return null;
}
if (filter(this))
{
return this;
}
for (int ic = _transitions.Count, i = 0; i < ic; ++i)
{
var t = _transitions[i];
var fa = t.To._FindFirst(filter);
if (null != fa)
{
return fa;
}
}
return null;
}
public FA FindFirst(FAFindFilter filter)
{
_Seen.Clear();
var result = _FindFirst(filter);
return result;
}It's almost the same as the other one except it short circuits once an FAFindFilter call returns true.
NFA to DFA Transformation
This is a bit of a trick. The powerset construction is easy-ish after you've implemented it a few times as I have although the range handling is a complicating wrinkle which I derived from Fare's implementation (by Nikos Baxevanis - license information with this project):
private static FA _Determinize(FA fa, IProgress<int> progress)
{
// initialize
int prog = 0;
progress?.Report(prog);
var p = new HashSet<int>();
var closure = new List<FA>();
fa.FillClosure(closure);
// gather our input alphabet
for (int ic = closure.Count, i = 0; i < ic; ++i)
{
var ffa = closure[i];
p.Add(0);
foreach (var t in ffa._transitions)
{
if (t.Min == -1 && t.Max == -1)
{
continue;
}
p.Add(t.Min);
if (t.Max < 0x10ffff)
{
p.Add((t.Max + 1));
}
}
}
var points = new int[p.Count];
p.CopyTo(points, 0);
Array.Sort(points);
++prog;
progress?.Report(prog);
var sets = new Dictionary<_KeySet<FA>, _KeySet<FA>>();
var working = new Queue<_KeySet<FA>>();
var dfaMap = new Dictionary<_KeySet<FA>, FA>();
var initial = new _KeySet<FA>();
var epscl = new List<FA>();
List<FA> ecs = new List<FA>();
List<FA> efcs = null;
_Seen.Clear();
fa._EpsilonClosure(epscl, _Seen);
for(int i = 0; i < epscl.Count;++i)
{
var efa = epscl[i];
initial.Add(efa);
}
sets.Add(initial, initial);
working.Enqueue(initial);
var result = new FA();
result.IsDeterministic = true;
result.FromStates = epscl.ToArray();
foreach (var afa in initial)
{
if (afa.IsAccepting)
{
result.AcceptSymbol = afa.AcceptSymbol;
break;
}
}
++prog;
progress?.Report(prog);
// powerset/subset construction
dfaMap.Add(initial, result);
while (working.Count > 0)
{
// get the next set
var s = working.Dequeue();
// get the next DFA out of the map
// of (NFA states)->(dfa state)
FA dfa = dfaMap[s];
// find the first accepting
// state if any, and assign
// it to the new DFA
foreach (FA q in s)
{
if (q.IsAccepting)
{
dfa.AcceptSymbol = q.AcceptSymbol;
break;
}
}
// for each range in the input alphabet
for (var i = 0; i < points.Length; i++)
{
var pnt = points[i];
var set = new _KeySet<FA>();
foreach (FA c in s)
{
// TODO: Might be able to eliminate the
// epsilon closure here. Needs testing
ecs.Clear();
if (!c.IsCompact)
{
// use the internal _EpsilonClosure
// method to avoid an extra call
// (basically inlining it)
_Seen.Clear();
c._EpsilonClosure(ecs, _Seen);
} else
{
ecs.Add(c);
}
for (int j=0;j<ecs.Count;++j)
{
var efa = ecs[j];
// basically if we intersect somewhere on the input alphabet,
// which we should, then we add the destination state(s) to the set
for (int k = 0; k<efa._transitions.Count;++k)
{
var trns = efa._transitions[k];
if (trns.Min == -1 && trns.Max == -1)
{
continue;
}
// TODO: can probably early out here
// if pnt > trns.Max?
if (trns.Min <= pnt && pnt <= trns.Max)
{
// skip the epsilon closure
// we don't need it
if (trns.To.IsCompact)
{
set.Add(trns.To);
}
else
{
if(efcs==null)
{
efcs = new List<FA>();
}
efcs.Clear();
_Seen.Clear();
trns.To._EpsilonClosure(efcs, _Seen);
for (int m = 0; m < efcs.Count; ++m)
{
set.Add(efcs[m]);
}
}
}
}
}
// less GC stress
_Seen.Clear();
}
// is this a new set or an
// existing one?
if (!sets.ContainsKey(set))
{
sets.Add(set, set);
// add another work item
working.Enqueue(set);
// make a new DFA state
var newfa = new FA();
newfa.IsDeterministic = true;
newfa.IsCompact = true;
dfaMap.Add(set, newfa);
var fas = new List<FA>(set);
// TODO: we should really sort fas
newfa.FromStates = fas.ToArray();
}
FA dst = dfaMap[set];
// find the first and last range to insert
int first = pnt;
int last;
if (i + 1 < points.Length)
{
last = (points[i + 1] - 1);
}
else
{
last = 0x10ffff;
}
// this should already be in sorted order
// otherwise we'd use AddTransition()
dfa._transitions.Add(new FATransition(dst,first, last));
++prog;
progress?.Report(prog);
}
++prog;
progress?.Report(prog);
}
// remove dead transitions (destinations with no accept)
foreach (var ffa in result.FillClosure())
{
var itrns = new List<FATransition>(ffa._transitions);
foreach (var trns in itrns)
{
var acc = trns.To.FindFirst(AcceptingFilter);
if (acc==null)
{
ffa._transitions.Remove(trns);
}
}
++prog;
progress?.Report(prog);
}
++prog;
progress?.Report(prog);
return result;
}As you can see from the TODOs, there's probably some room for improvement, but I've already optimized it over several parts. I don't really care if this particular bit of code is that readable because the algorithm is nasty and even if the code was written more accessibly, it would still be confusing. It needs to be as fast as it can be, because it's already a long process for large machines.
Unfortunately, the minimization is something I don't understand. I can't even tell which of the 3 or so algorithms for that that it's using. Again, I borrowed the implementation from Fare, wholesale this time. It works, so I can't complain, but man is it hard to follow! I'm not going to post it here in the interest of sanity because it's very long and so confusing it probably won't add much value here. It's not like I can walk you through it. The meat is in _Minimize().
Moving Through a Machine
FillMove() (any machine) and Move() (DFA only) navigate a machine based on inputted codepoints:
public static IList<FA> FillMove(IList<FA> states,
int codepoint,
IList<FA> result = null)
{
_Seen.Clear();
if (result == null) result = new List<FA>();
for (int q = 0; q < states.Count;++q)
{
var state = states[q];
for (int i = 0; i < state._transitions.Count; ++i)
{
var fat = state._transitions[i];
// epsilon dsts should already be in states:
if (fat.Min == -1 && fat.Max == -1)
{
continue;
}
if(codepoint<fat.Min)
{
break;
}
if (codepoint <= fat.Max)
{
fat.To._EpsilonClosure(result, _Seen);
}
}
}
_Seen.Clear();
return result;
}Basically, all we're doing above is checking a codepoint against the transitions. We get away with a lot because transitions are sorted. In this case, we can early out as soon as we're out of range instead of scanning the entire set of transitions. We skip epsilon transitions since the caller should have already followed them. We take the epsilon closure of each destination state. Note that we use _Seen for all of them. That's because we don't want any duplicates across the board.
Move() does similar but it doesn't have to use lists or deal with overlapping ranges to different destinations so it's considerably more performant:
public FA Move(int codepoint)
{
if (!IsDeterministic)
{
throw new InvalidOperationException(
"The state machine must be deterministic");
}
for(int i = 0;i<_transitions.Count;++i)
{
var fat = _transitions[i];
if(codepoint<fat.Min)
{
return null;
}
if(codepoint<=fat.Max)
{
return fat.To;
}
}
return null;
}Array Serialization and Deserialization
ToArray() turns a state machine into an int[] array:
public int[] ToArray()
{
var working = new List<int>();
var closure = new List<FA>();
FillClosure(closure);
var stateIndices = new int[closure.Count];
// fill in the state information
for (var i = 0; i < stateIndices.Length; ++i)
{
var cfa = closure[i];
stateIndices[i] = working.Count;
// add the accept
working.Add(cfa.IsAccepting ? cfa.AcceptSymbol : -1);
var itrgp = cfa.FillInputTransitionRangesGroupedByState(true);
// add the number of transitions
working.Add(itrgp.Count);
foreach (var itr in itrgp)
{
// We have to fill in the following after the fact
// We don't have enough info here
// for now just drop the state index as a placeholder
working.Add(closure.IndexOf(itr.Key));
// add the number of packed ranges
working.Add(itr.Value.Count);
// add the packed ranges
working.AddRange(FARange.ToPacked(itr.Value));
}
}
var result = working.ToArray();
var state = 0;
// now fill in the state indices
while (state < result.Length)
{
++state;
var tlen = result[state++];
for (var i = 0; i < tlen; ++i)
{
// patch the destination
result[state] = stateIndices[result[state]];
++state;
var prlen = result[state++];
state += prlen * 2;
}
}
return result;
}We have to make two passes. On the first pass through the machine, we fill in all the basic state information into the working list. However, at this point, we don't know the final index for each state so we can't fill in the destination jumps. Instead, we fill stateIndices with the absolute working array index for each state. On the next pass, we walk the machine again so we can find the destination states and replace with their corresponding index in the array before returning it.
To deserialize, we use FromArray():
public static FA FromArray(int[] fa)
{
if (null == fa) throw new ArgumentNullException(nameof(fa));
if (fa.Length == 0)
{
var result = new FA();
result.IsDeterministic = true;
result.IsCompact = true;
return result;
}
// create the states and build a map
// of state indices in the array to
// new FA instances
var si = 0;
var indexToStateMap = new Dictionary<int, FA>();
while (si < fa.Length)
{
var newfa = new FA();
indexToStateMap.Add(si, newfa);
newfa.AcceptSymbol = fa[si++];
// skip to the next state
var tlen = fa[si++];
for (var i = 0; i < tlen; ++i)
{
++si; // tto
var prlen = fa[si++];
si += prlen * 2;
}
}
// walk the array
si = 0;
var sid = 0;
while (si < fa.Length)
{
// get the current state
var newfa = indexToStateMap[si];
newfa.IsCompact = true;
newfa.IsDeterministic = true;
// already set above:
// newfa.AcceptSymbol = fa[si++];
++si;
// transitions length
var tlen = fa[si++];
for (var i = 0; i < tlen; ++i)
{
// destination state index
var tto = fa[si++];
// destination state instance
var to = indexToStateMap[tto];
// range count
var prlen = fa[si++];
for (var j = 0; j < prlen; ++j)
{
var pmin = fa[si++];
var pmax = fa[si++];
if (pmin == -1 && pmax == -1)
{
// epsilon
newfa.AddEpsilon(to, false);
}
else
{
newfa.AddTransition(new FARange(pmin, pmax), to);
}
}
}
++sid;
}
return indexToStateMap[0];
}Really, all we're doing here is first creating all the FA instances we need, and setting their accept symbols, and then filling in the transitions from the array.
Creating Lexers
ToLexer() can be used to create a lexer out of a series of machines. It's pretty much a convenience method, especially when creating a DFA lexer from a series of expressions.
public static FA ToLexer(IEnumerable<FA> tokens,
bool makeDfa = true,
bool compact = true,
IProgress<int> progress = null)
{
var toks = new List<FA>(tokens);
if (makeDfa)
{
// first minimize the inner machines
for (int i = 0; i < toks.Count; i++)
{
toks[i] = toks[i].ToMinimizedDfa(progress);
}
}
// create a new root state.
var result = new FA();
for (int i = 0; i < toks.Count; i++)
{
result.AddEpsilon(toks[i], compact);
}
if (makeDfa && !result.IsDeterministic)
{
return result.ToDfa(progress);
}
else
{
return result;
}
}You cannot safely call ToMinimizedDfa() on the root of a lexer, which complicates making an efficient DFA out of it. This function first minimizes each passed in machine before creating the root of the lexer. If necessary and specified, it will convert the root to a DFA, basically removing any conflicts in the root.
Parsing
Parsing is a bit involved. We don't really have room to explore the code as there is an awful lot of it. Don't worry, it's not that interesting and I can describe it here. Basically, what it does is scan through an input string using StringCursor, which holds a cursor over UTF-32 codepoints pulled from a string and tracks the position. As it encounters elements of the expression, it uses the Thompson construction methods to build out the machine. It's simple in concept. The trickiest part is parsing ranges because the range syntax is so complicated.
ToString Magic
ToString() by itself isn't that interesting until you start passing format specifiers. "e" and "r" can turn a state machine back into a regular expression. It should be noted that while the expressions are correct, the result can be convoluted and somewhat redundant sometimes, especially when it comes to looping constructs. "r" attempts to reduce the expression to something a bit more readable, but is much more resource hungry, and I'm still improving it.
It's another long one we won't get into here other than to describe the overall function of it. First, it constructs a list of edges of the machine. These edges contain from and to states plus a string indicating an expression. At first, those strings are just range sets from one state to the next. As we move through them, we eliminate states by concatenating an expression from a state targeted for removal to any transition that leads to it, and then on those transitions we change the destination state to the destination state in the targeted class's transition, essentially skipping it and orphaning it.
As it does so, it handles loops specially. If it encounters loops, it adds them to its own list of loop expressions for turning into a string later. Any looping transitions are not evaluated in the removal loop described in the previous paragraph.
ToString("r") is a bit different. It uses the RegexExpression Abstract Syntax Tree model to represent the expression internally so it can call Reduce() on the expression, which attempts to simplify it. Finally, it renders that to a string. In effect, it does everything ToString("e") does but differently (through the AST) and with extra steps.
I would really like to thank David Wolever for creating his state machine to expression code in Go. I tried to implement this for years unsuccessfully, and none of the resources I could find describing the algorithm were complete and accurate enough to code off of. Finally, I stumbled across his work, learned a bit of Go, and now I understand the process. It's great!
Graphing States
I produced the graphs in these articles using RenderToFile() and RenderToStream() off of FA.
These functions automate the Graphviz dot executable from the command line, which is responsible for turning input in the dot language into output in the specified image format.
First let's look at RenderToFile():
public void RenderToFile(string filename, FADotGraphOptions options = null)
{
if (null == options)
options = new FADotGraphOptions();
string args = "-T";
string ext = Path.GetExtension(filename);
if(0==string.Compare(".dot",
ext,
StringComparison.InvariantCultureIgnoreCase)) {
using (var writer = new StreamWriter(filename, false))
{
WriteDotTo(writer, options);
return;
}
} else if (0 == string.Compare(".png",
ext,
StringComparison.InvariantCultureIgnoreCase))
args += "png";
else if (0 == string.Compare(".jpg",
ext,
StringComparison.InvariantCultureIgnoreCase))
args += "jpg";
else if (0 == string.Compare(".bmp",
ext,
StringComparison.InvariantCultureIgnoreCase))
args += "bmp";
else if (0 == string.Compare(".svg",
ext,
StringComparison.InvariantCultureIgnoreCase))
args += "svg";
if (0 < options.Dpi)
args += " -Gdpi=" + options.Dpi.ToString();
args += " -o\"" + filename + "\"";
var psi = new ProcessStartInfo("dot", args)
{
CreateNoWindow = true,
UseShellExecute = false,
RedirectStandardInput = true
};
using (var proc = Process.Start(psi))
{
if (proc == null)
{
throw new NotSupportedException(
"Graphviz \"dot\" application is either not installed or not in the system PATH");
}
WriteDotTo(proc.StandardInput, options);
proc.StandardInput.Close();
proc.WaitForExit();
}
}What we're doing here is gathering the file extension from the passed in path and using that to determine the output file format. Then we prepare the command line arguments. Finally, we create a new ProcessStartInfo instance, filling it with the relevant data before calling on Process to run the thing. Once it runs, it feeds the input directly to dot's stdin. Dot does the actual file writing. This routine blocks but I may eventually make an async method that can return before the image is rendered.
RenderToStream() is similar except we take the format as a string argument (which may change to an enum later), and we read the stream out of dot's stdout.
public Stream RenderToStream(string format,
bool copy = false,
FADotGraphOptions options = null)
{
if (null == options)
options = new FADotGraphOptions();
if(0==string.Compare(format,
"dot",
StringComparison.InvariantCultureIgnoreCase))
{
var stm = new MemoryStream();
using(var writer = new StreamWriter(stm)) {
WriteDotTo(writer, options);
stm.Seek(0,SeekOrigin.Begin);
return stm;
}
}
string args = "-T";
args += string.Concat(" ", format);
if (0 < options.Dpi)
args += " -Gdpi=" + options.Dpi.ToString();
var psi = new ProcessStartInfo("dot", args)
{
CreateNoWindow = true,
UseShellExecute = false,
RedirectStandardInput = true,
RedirectStandardOutput = true
};
using (var proc = Process.Start(psi))
{
if(proc==null)
{
throw new NotSupportedException(
"Graphviz \"dot\" application is either not installed or not in the system PATH");
}
WriteDotTo(proc.StandardInput, options);
proc.StandardInput.Close();
if (!copy)
return proc.StandardOutput.BaseStream;
else
{
var stm = new MemoryStream();
proc.StandardOutput.BaseStream.CopyTo(stm);
proc.StandardOutput.BaseStream.Close();
proc.WaitForExit();
return stm;
}
}
}The creation of the input to feed dot is long and ugly. The dirty truth of it is that it has survived so many incarnations of my FA engines that the code is rotten and needs to be rewritten. The thing is, it works pretty well, and does an awful lot. Changing it with cleaner code will be a lot of effort. At any rate, I'm not going to post the code here because it's extremely long.
What's Next?
In the next installment, we will go over the code generation facilities in VisualFA.Generator.
History
- 20th January, 2024 - Initial submission