Pck/FA: A Regular Expression and Finite State Engine in C#
Updated on 2019-08-05
A regex and finite state engine as part of PCK
Introduction
The Parser Construction Kit (PCK) is a large project, with many different components. Rather than explore all of the source code at once, we'll work on an area at a time. Each of these areas is useful in its own right, but all contribute to PCK's capabilities.
This component is the finite automata engine, FA. What it is, in a nutshell, is a regular expression and tokenizing library. However, it also has some unique features, like being able to express or represent regular expressions as an abstract syntax tree, provided as a DOM which makes it potentially capable of representing many different styles of DFA regular expression.
We can't use .NET's regular expression engine for efficient lexing. It just wasn't designed for it and carries a number of drawbacks, including backtracking, which are unacceptable for efficient parsers. Pck/FA includes a simple, DFA based regular expression engine, as well as a more general finite state machine engine. You can use the general FA for doing things like computing states in an LR parser or driving a workflow engine with complicated reconciliation paths.
Unlike my previous regular expression engine, this one doesn't generate any code. It doesn't really need to. It simply renders an array for the state machine table, and you can pass that to a CodeDOM serializer like the one I provide here, which will then render it in any compliant language.
Background
Regular expressions are dumb. They don't know anything about the input, they have a very simple grammar, and there's not a whole lot of operations you can perform.
Regular expressions are shortsighted. They are very nearly blind throughout the lexing process - only knowing which state they are in and what the next character is at any point.
Regular expressions are elegant. They do exactly what they need to do and no more. A character is examined exactly once, the language is concise, and the expressive power belies its simplicity.
We're going to take advantage of the dumb and short sighted parts to keep the code simple. Dumb is good. Dumb is easy to test. Dumb is easy to code. Short sightedness, if you can get away with it, is very efficient.
I don't want to give a regular expression tutorial so I made my engine POSIX-like. It doesn't yet support POSIX named character classes (although it recognizes them) and it doesn't support a few of the escape character classes (like word break) yet, or collation and equivalence classes but it's close, if not interchangeable for most real world cases. If it doesn't work with a POSIX expression, consider it a bug.
If you need a regex tutorial, check here.
Regular expressions resolve to jump tables over enumerators. Basically, it's like this:
q1:
if((pc.Current>='0'&& pc.Current<='9')||
(pc.Current>='A'&& pc.Current<='Z')||
(pc.Current=='_')||
(pc.Current>='a'&& pc.Current<='z')) {
sb.Append((char)pc.Current);
pc.Advance();
goto q1;
}
return new System.Collections.Generic.KeyValuePair
<System.String,string>("id",sb.ToString());At least if we were to generate the code. That's state 1, transitioning to itself on a letter, a digit, or underscore, or otherwise accepting. In practice, we don't really do that kind of code generation, since the array table based code is faster in .NET, but it's simple enough.
It's easier though, to look at a regular expression's state machine as a directed graph rather than code:
Here's a graph for the regular expression matching a C# style identifier [A-Z_a-z][0-9A-Z_a-z]*
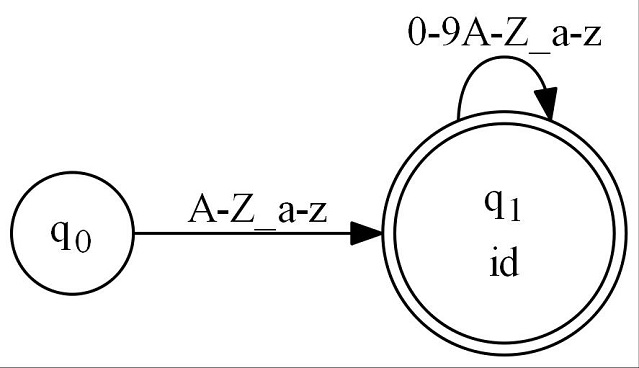
We saw the "generated code" for state q1 from above. Study both that and the graph, and you should see where they come together. This is a really simple graph. A more complicated graph is easy, just make a more complicated regular expression.
Now you should be able to see how the graphs resolve to jump tables. The real trick is getting an expression to resolve to a graph. It's not simple, but it's easier than it sounds once you know how.
Let's take a step back, because the above graph isn't the whole story. What I haven't shown you yet is that we made it from another graph!
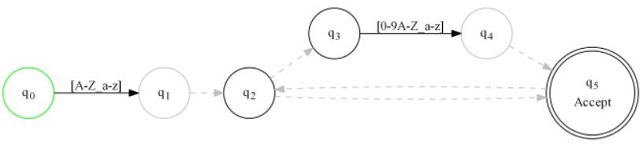
The state in green just represents the starting state. We don't care about that right now. As for the rest of the graph, it has a lot more states, and strange dashed gray lines. Let's talk about that.
Traditionally, before moving along a black line, we must wait for a single input, which we then consume while advancing along the line toward the arrow.
With the gray dashed lines, called "epsilon transitions" we don't have to wait for any input. We just move, and that means we may wind up in multiple states at once since we move along every dashed gray path we see from where we are.
If you're clever and caffeinated, your first question might be "how in the world do we make the generated code from above do that?" - and it's a great question.
The answer is we don't. There's a mathematical property of a graph like this: Each of these has one equivalent graph with no dashed lines in it - by equivalent, I mean one that matches the same input. So for every one of these that you can imagine, there exists a correlating graph with no dashed lines that is its equal.
All we have to do is find it. We use a technique called powerset construction to do that. The math is kind of weird but the fagui app can visualize it to a degree. The graph on the top panel of the app is the untransformed FA - we call it the NFA. And the one on the bottom panel in the app is the equivalent graph with no dashed lines, we'll call it the DFA.
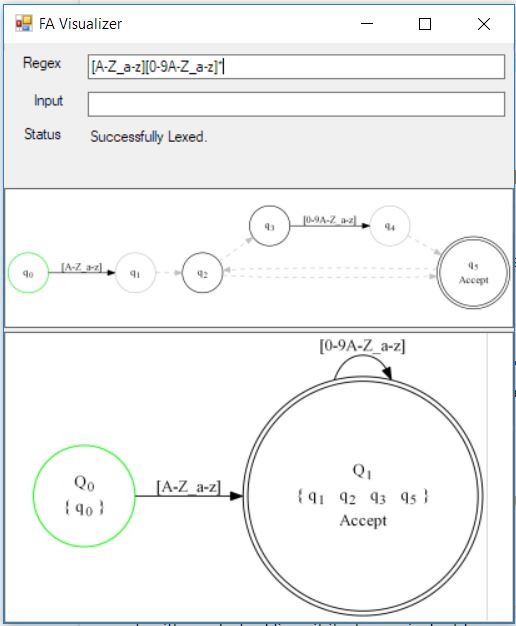
You can see on the bottom that the states have a list of all the states from the top which they represent. It's typical for one state from the bottom (the DFA) to represent multiple states from the top (the NFA). In fact, that's how the powerset construction works. It examines all possibilities of the graph and creates new states to represent those possibilities. Fortunately, the ToDfa() function handles the grotty details.
You'll note that state q4 is missing from Q1's state list on the bottom. It got removed when duplicate states were removed (via TrimDuplicates()). The reason it was removed is because it causes a duplicate in the resulting DFA but that step wasn't shown above, and isn't critical - duplicate states don't break these machines, they're just redundant.
Now, I've told you about this magic graph transformation, but I still haven't covered how we got the graph with the dashed lines in it - from now on, just called the NFA. These are composed using Thompson's construction algorithm, which defines some basic graph constructs which you can then compose together to create compound graphs. Thompson's algorithm basically requires that every construction has exactly one state that "accepts". That is, one state with the double-circle from above.
Thompson's construction algorithm
First, it might help to show you the basic data structure of a state:
class CharFA {
public IDictionary<char,CharFA> Transitions {get;}=new Dictionary<char,CharFA>();
public ICollection<CharFA> EpsilonTransitions {get;}=new List<CharFA>();
public bool IsAccepting {get;set;}=false;
public string AcceptSymbol {get; set;}=null;
}Each transition is keyed by a single input character and leads to another instance of the CharFA. Each epsilon transition (dashed line) is simply represented by the presence of a destination state in the collection.
If IsAccepting is true, the state is a double-circle in the graph and the input captured so far once it lands there is considered valid, even if it can't match any further. The AcceptSymbol isn't strictly necessary for the purpose of demonstration, but it just gives us a label to mark the accept with. We can ignore it for now.
The Transitions property maps exactly to our jump table for each state. The EpsilonTransitions also "virtually" jump concurrently, but we want to eventually remove all those from the graph since rendering that in code would be a special kind of nightmare.
Let's build a set of states to represent a graph for the simple expression "foo" manually in code. Make sure Graphviz is installed, fire up VS with a new console app in .NET Core - add a reference to pck.fa, and then try this:
using CharFA = Pck.CharFA<string>;
class Program
{
static void Main(string[] args)
{
var foo = new CharFA();
var foo2 = new CharFA();
var foo3 = new CharFA();
var foo4 = new CharFA();
foo.Transitions.Add('f', foo2);
foo2.Transitions.Add('o', foo3);
foo3.Transitions.Add('o', foo4);
foo4.IsAccepting = true;
// write a pretty picture!
foo.RenderToFile(@"..\..\..\foo.jpg");
return;
}
}Which outputs foo.jpg to the project directory:

Now, let's alter the code (and the graph) slightly by making it accept any number of trailing "o"s:
...
foo.Transitions.Add('f', foo2);
foo2.Transitions.Add('o', foo3);
foo3.Transitions.Add('o', foo4);
foo4.IsAccepting = true;
foo4.EpsilonTransitions.Add(foo3); // <-- add this line
foo.RenderToFile(@"..\..\..\foo.jpg");
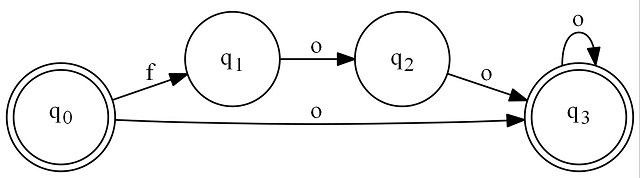
...Now foo looks like this:

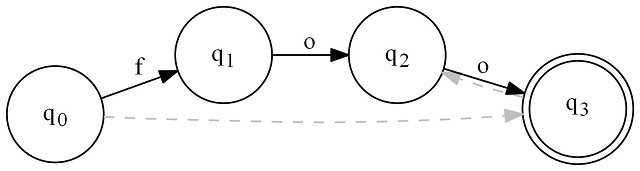
Now, let's modify our code once again to make our expression accept an empty string:
...
foo.Transitions.Add('f', foo2);
foo2.Transitions.Add('o', foo3);
foo3.Transitions.Add('o', foo4);
foo4.IsAccepting = true;
foo4.EpsilonTransitions.Add(foo3); // (from before)
foo.EpsilonTransitions.Add(foo4); // <-- now add this line
foo.RenderToFile(@"..\..\..\foo.jpg");
...
Do you see that? This is how our state graphs ultimately get constructed. Don't do it manually like this though. Use the static methods like Literal(), Set(), Or(), Repeat(), Concat() and Optional().
Alternatively, you can use the RegexExpression DOM, but that's a bit heavy handed, unless you're parsing.
One last thing: Let's transform that graph into its more efficient DFA counterpart with ToDfa().
using CharFA = Pck.CharFA<string>;
class Program
{
static void Main(string[] args)
{
var foo = new CharFA();
var foo2 = new CharFA();
var foo3 = new CharFA();
var foo4 = new CharFA();
foo.Transitions.Add('f', foo2);
foo2.Transitions.Add('o', foo3);
foo3.Transitions.Add('o', foo4);
foo4.IsAccepting = true;
foo4.EpsilonTransitions.Add(foo3);
foo.EpsilonTransitions.Add(foo4);
foo = foo.ToDfa(); // added this line
foo.RenderToFile(@"..\..\..\foo.jpg");
return;
}
}
If you follow the lines of each graph carefully, you'll see that they are equivalent.
Using the Code
This code turns regular expressions into directed graphs like the above. It can then turn the graphs into array based transition tables. It can render the graphs with Graphviz, or produce those arrays to be worked with by external code.
There are two major state machine classes in this library, FA<TInput,TAccept>, and a "specialization" of FA<char,TAccept> called CharFA
The latter is a full regex engine and optimized significantly for characters, while the former allows you to use input types other than char.
The CharFA
The FA<TInput,TAccept> class contains the API subset that isn't specifically tied to characters, regular expressions and range matching.
There's a Lex() method as well, but it's primarily for debugging or examining a state machine in action. Lexer code usually varies depending on the application and while this method works, it just won't return enough information (like line and position) to be suitable for most real-world situations. Code generation is handled by outside tools that use this library.
In my previous regular expression submission, the code generation and runtime lexing routines were included in the main class. In this distribution, they are in a separate project. The reason being I found that in practice, each lexer is different enough so as to warrant its own specific lexing routine which is a variation of the standard. So instead, the main FA class simply generates the DFA tables as arrays. It's up to whoever consumes the array to do something useful with it, like generate code or lex a document. I've also provided fagen within the pckw project which will generate tokenizer code from them.
This code also provides an Abstract Syntax Tree or AST for a given regular expression. So you can parse a regular expression into the tree, and then examine the individual components that make up the expression, like the ors and the concatenations and the repeats. You can potentially take that tree and use it to render to different regular expression formats like the CodeDOM does for code. In fact, this is an analog to the AST provided by the CodeDOM but for working with regular expressions. Instead of CodeExpression and CodeUnaryExpression for example, you have RegexExpression and RegexUnaryExpression. You can use the RegexExpression's Parse() method to get a regular expression AST from a string, and you can use the ToFA
var ast = RegexExpression.Parse(RegexTextBox.Text);
var fa = ast.ToFA("Accept");Finally, there's one area of the extensive API we haven't covered at all, and that's the LexDocument API. This API exposes yet another document object model, this time for PCK specification files. These are much like flex/lex spec files (".l" extension) and can be used to create tokenizers/lexers to scan input.
These files can also have grammar rules, but those are ignored by the LexDocument API - the grammar rules are made to be read by parser generators, not lexer generators. The two formats in the document can intermingle, but only the lexer rules and attributes are picked up by this API. PCK files themselves are almost always machine generated from another format - often XBNF, but that's a topic for another article.
The format is line based with a lexer rule being:
MyRuleName= 'myregex'We'll cover attributes in the future. They aren't directly relevant here, but are used by various tools to change aspects of things like code generation or special behaviors.
History
- 3rd August, 2019 - Initial submission